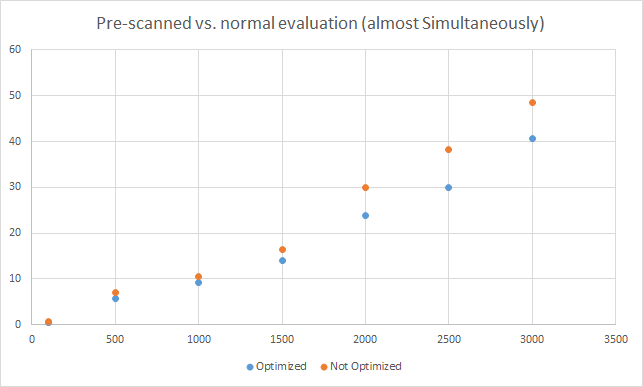
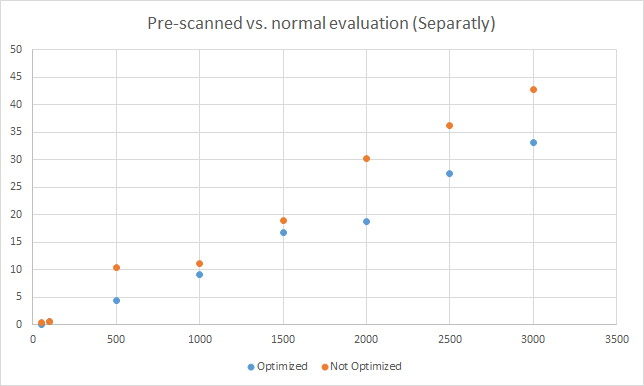
The requirement of performing several thousands of calculations (for example, during integration) led to the optimization with pre-scanned expressions. But the aim to make Mathos Parser even faster still remained. Now, I would like to introduce you to a new project of Mathos Project – Mathos Expression Compiler, based on the math tokenizer and parser logic of Mathos Parser.
This API allows you to parse an expression and “store” it as CIL code. Then, using ILAsm, you can generate a new assembly that will contain your expression entirely parsed. The only operation that occurs at runtime is the insertion of values into the variables that you declared and the operation on that variable value. To make it even faster, most of the calculations are already done before the runtime, for example, x+3+5 would be stored as x+8.
In this scenario, the time consideration can be important. Even if it is faster to execute CIL instructions, the compilation process can take some time. This has not been tested yet. The process is illustrated below:
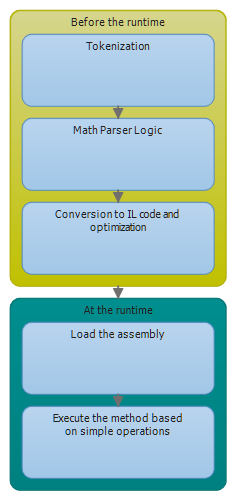
This is a very simplified way of looking at it but the point is to always test Mathos Parser together with Mathos Expression Compiler and make an estimate of how much time would be saved in different scenarios. It all depends on the context. But note, that
A performance hit is incurred only the first time the method is called. All subsequent calls to the method execute at the full speed of the native code because verification and compilation to native code don’t need to be performed again. //p. 12. Jeffrey Richter. CLR via C# 3rd Edition
So, if you plan to execute the function trillion times, it might be a good a idea to keep in mind the Expression Compiler as a better alternative, because at that point, the compilation time will be negligible.
Now, back to the features. It was mentioned in the beginning that it is based on the Mathos Parser. Note, in terms of features, Mathos Expression Compiler has at this point only a subset of those of Mathos Parser. At this point, you cannot have functions as sin, cos, and your own custom functions, but this will be changed in the nearest future.
There are also some changes to the way operators work. To declare an operator properly, you should use the variables OperatorList, OperatorAction, and OperatorActionIL. Below, a simple example of addition operator:
OperatorList.Add("+"); // addition
OperatorActionIL.Add("+", "call valuetype [mscorlib]System.Decimal [mscorlib]System.Decimal::op_Addition(valuetype [mscorlib]System.Decimal,valuetype [mscorlib]System.Decimal)");
OperatorAction.Add("+", (x, y) => x + y);
Comparison operators are a bit more tricky. An example of greater than operator is shown below:
OperatorList.Add(">"); // greater than
OperatorActionIL.Add(">", "call bool [mscorlib]System.Decimal::op_GreaterThan(valuetype [mscorlib]System.Decimal,valuetype [mscorlib]System.Decimal)\r\n" +
"brtrue.s q@\r\n" +
"ldc.i4.0 \r\n" +
"br.s p@\r\n"
+ "q@: ldc.i4.1\r\n"
+ "p@: nop\r\n"
+ "call valuetype [mscorlib]System.Decimal [mscorlib]System.Decimal::op_Implicit(int32)");
OperatorAction.Add(">", (x, y) => x > y ? 1 : 0);
For those who understand IL, the @ sign might seem a bit strange. It is simply a way to tell the stack count to the if statement (in the compilation process).
When you actually generate an expression, this is how your IL code for that expression might look:
var mp = new Mathos.ILParser.ILMathParser();
mp.LocalVariables.Add("x");
mp.LocalVariables.Add("y");
string a = mp.Parse("(x(3x))");
Will return (only IL for the expression):
.maxstack 5 .locals init(valuetype [mscorlib]System.Decimal, valuetype [mscorlib]System.Decimal) ldc.i4 3 ldc.i4 0 ldc.i4 0 ldc.i4 0 ldc.i4 0 newobj instance void [mscorlib]System.Decimal::.ctor(int32,int32,int32,bool,uint8) stloc.0 ldloc.0 ldarg.0 call valuetype [mscorlib]System.Decimal [mscorlib]System.Decimal::op_Multiply(valuetype [mscorlib]System.Decimal,valuetype [mscorlib]System.Decimal) stloc.1 ldloc.1
When you have the IL code, you should name the output executable(or dll) as MathosILParser, otherwise, you might get an error. In future, an option will be added to customize the name of the output file, but at this point, please use RegEx (or replace option) to change the MathosILParser.exe to something else (in the IL code).
Your function can later by called as shown below. Note, I am not using reflection at all.
decimal result = Mathos.ILFunction.Parse(3, 2);
I hope this short guide was helpful, even if it might be a bit messy. If you have performed any testing related to speed or if you want to show some examples, please feel free to comment or contact me.