My new website (artemlos.net) is now finished, so all the new blog posts will be found at https://artemlos.net/blog/ instead.
General thoughts about time management
[Originally published at https://www.kth.se/profile/204929/page/general-thoughts-about-time-management/]
Being able to plan your studies and time in general is important to be productive. But why do people really do it? Why do we want to stay productive? One possible answer to this is the realization of the tasks that have to be done and the time that is at our disposal. Once the number of tasks increases, we soon realize that time is a scarce resource and has to be used wisely. In this post, we are going to look at a purely tactical approach, how it can be affected by time pressure, and finally how the university has contributed to a combination of both tactical and strategical thinking and how this is related to knowledge from computer science.
Throughout the high school and the first year at the university, I’ve been really into time management. Back then, I think I viewed the planning from a tactical perspective, i.e. during the day I had a set of tasks (such as homework) that were split up into 45 minute sessions, accompanied by 15 minutes break, later by 30 minutes break, and later I switched the subject, even if I had things left. This was suggested by my ToK teacher Ric Sims. I must admit that I did not follow it all the time, but at least I had the time structured into intervals with breaks. At that time, my approach to homework was pragmatic (as far as I can recall), i.e. I prioritized them and executed them as some sort of TODO list.
Later, once the finals were approaching, I started to do other tasks such as doing past papers, rewriting the syllabus (this was not a good idea I think, but allowed me to memorize key concepts), and so on. Suddenly, as they got closer, I had detailed plans of what has to be done during a certain month, a certain week, and so forth; strategical thinking was emerging. For the finals, I came up with a detailed schedule to utilize as much time as possible (the Excel file: Finals approaching). To sum up, as time gets scarce, you tend to plan more to ensure that you use it effectively.
Now, at the university, planning gets even more important. I tend to plan several months and even years ahead (by specifying goals, a strategy). For instance, last year, my plan was to focus onMulti Variable Caclulus, a subject that I was not supposed to study in year 1. Now, my plan (this year) is to focus on my project – Serial Key Manager – and apply to Student Inc. Once the direction (strategy) is specified, it is easy to move forward by breaking the goals into smaller ones, and ultimately have a concise list of tasks; solving these is a question of tactical nature. As an example, this week, I tried to write down all the tasks in an Excel sheet, prioritize them, and complete them one by one (see fig 1).
This gave me a clearer picture and allowed me to organize my time more effectively. This weekly plan however, can be generalized to a monthly plan, a yearly plan and so forth as well as broken down in to smaller components that take time into consideration.
Some computer scientist will point out that this kind of reasoning is related to modulation and abstraction. That is, the yearly plan can be thought of like Python, the monthly plan as Java, the weekly plan as C++ and the daily one as Assembler. It’s interesting that we can combine our knowledge from different disciplines to achieve great results!
Surely, planning is crucial to a successful use of our time. But, it’s also important to understand that different planning approaches have to be applied depending on the type of planning (such as strategical or tactical thinking). All of this helps us to cope with tasks considering that time is a scarce resource. However, we should always remember that for a good execution of tasks, we need to be balanced (don’t overestimate) and reflective (try to find a strategy that works best for you)!
Plan for future article: Next time, my intention is to look at ways to manage the time when you are executing a task. What other alternatives are there(such as Pomodoro technique)? How do we reduce procrastination? But for now, please let me know your thoughts about the current post! 🙂
Continuation of my Calculus Journey
Introduction
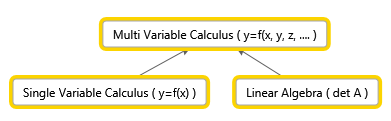
During the two periods (from January), I’ve been working with with an interesting branch of mathematics – Multi Variable Calculus. Besides, I was studying Linear Algebra (see my other post) and Numerical Methods. Since I’m not actually supposed to study it in year 1, it was quite difficult when I needed knowledge of Linear Algebra to be able to understand certain concepts. In addition, there were clashes with other lectures and practice sessions, so I was effectively left with the course literature and other resources. This put me into a situation where I had to obtain the knowledge on my own and ensure that I understood the concepts. A friend of my (who took this course also) was sitting in the library and used other books that were available. My strategy was to use the original book in addition to the resources available online (such as other literature, videos, and Math SE). I think both strategies were really helpful in the study of Multi Variable Calculus. Here’s one thing I thought about two months after the course start:
$$ \displaystyle \underset{{Time\to \infty }}{\mathop{{\lim }}}\,Calculus=Physics$$
This is the connection between the subjects:
Spaces (3 to n space)
It’s quite convenient to translate real world problems into mathematical models, manipulate the data and interpret the result in a real world context. Since we live in a 3 dimensional world (at least, that’s the way many of us interpret it), many might already be familiar with \(x,y,z\) coordinate system that allows us to express location of any object. But, if we were able to go from having things expressed in \(2\)d to \(3\)d, why not just go directly to \(4\) or even \(n\) space? Suddenly, we need to ensure that our definitions of concepts such as distance, neighborhood are clear and make sense even when we leave \(3\) space.
Let’s look at neighborhood. If we simply think about a line with numbers, we could say that neighbors to a number \( p\) are numbers in the interval \((p-r,p+r)\). So, if we set \(r=2\) and choose \(p\) to be \(3\), the interval is \((1,5)\). So, \(1,2,4,5\) are some of the neighbors to \(3\) at a distance \(r\). Now, you might wonder why we look at the neighborhood. That’s simply to illustrate how things change when we add another dimension. Imagine that we are asked about the neighborhood to a point \(p\) in \( 2\) space instead. Instead of a line, we get a disk with a radius \(r\) centered at point \(p\). In \(3\) space, it’s a ball centered at \(p\) of radius \( r\). The same trend will be observed when we started to look at the domain. For simple functions, the domain is a set of points on a line. For two variables, it is two-dimensional object and so on.
Cylindrical Coordinates
In single variable calculus, the polar coordinates might ring a bell. Cylindrical coordinates are quite similar. We basically perform the following substitution:
$$\left\{ \begin{gathered}
x = r\cos \theta \hfill \\
y = r\sin \theta \hfill \\
z = z \hfill \\
\end{gathered} \right.$$
The convention is that \(r\ge 0\) and that \(0 \le \theta \le 2\pi\). You might ask why we would need such coordinates? I had a similar question when I confronted them. They were more annoying than useful at the first sight (but spherical coordinates were even worse). However, once I started to deal with integrals with “strange” domains, they were a great relief. It will also be useful to know that the volume element is:
$$ \displaystyle dV=rdrd\theta dz$$
Spherical Coordinates
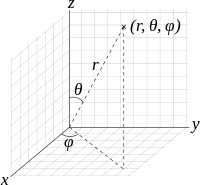
Spherical coordinates, as cylindrical coordinates, are based on a substitution that contains trigonometric functions. In this case, the substitution is:
$$ \displaystyle \left\{ \begin{array}{l}x=R\sin \phi \cos \theta \\y=R\sin \phi \sin \theta \\z=R\cos \phi \end{array} \right.$$
The convention is that \(\displaystyle R\ge 0,\quad 0\le \phi \le \pi ,\quad 0\le \theta \le 2\pi \). The volume element that proves to be useful later is \(\displaystyle dV={{R}^{2}}\sin \phi dRd\phi d\theta \).
Vector Functions
In many physics scenarios that appear in high school textbooks, problems are reduced two one/two dimensions. However, all of us know that the world has both a width, a breadth and a height. So, it can be useful to represent objects using three coordinates. If we disregard relativity for a moment, let’s say that the position of a particle is determined by time \(t\). In other words,
$$ \displaystyle \left\{ \begin{array}{l}x=x(t),\quad y=y(t),\quad z=z(t)\\\vec{r}=(x(t),y(t),z(t))\end{array} \right.$$
So, you give me a time \(t\) and I will be able to tell you where the particle is. In the same manner, we can express velocity and acceleration. That is,
$$ \displaystyle \vec{v}=\frac{d\vec{r}}{dt}=\left( \frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt} \right),\qquad \vec{a}=\frac{{{d}^{2}}\vec{r}}{d{{t}^{2}}}=\left( \frac{{{d}^{2}}x}{d{{t}^{2}}},\frac{{{d}^{2}}y}{d{{t}^{2}}},\frac{{{d}^{2}}z}{d{{t}^{2}}} \right)$$
Both velocity and acceleration have a magnitude and a direction, whereas speed has a magnitude only. However, in practice, we hear people use velocity and speed interchangeably. Anyway, given a velocity vector, it’s quite easy to find the speed, namely by taking the (euclidean) norm. That is,
$$ \displaystyle v=||\vec{v}||=\left\| \frac{d\vec{r}}{dt} \right\|={{\left( \frac{dx}{dt} \right)}^{2}}+{{\left( \frac{dy}{dt} \right)}^{2}}+{{\left( \frac{dz}{dt} \right)}^{2}}$$
Example: An object is moving to the right along the plane \(y=x^2\) with constant speed \(v=5\). Find \(\vec v\) at $(1,1)$.
Solution: We simply need to express the movement in the plane as a vector, so since we \(y=x^2, \quad \vec r =(x,x^2)\). By taking the derivative of \(\vec r\), we get:
$$ \displaystyle \vec{v}=\frac{d\vec{r}}{dt}=\left( \frac{dx}{dt},2x\frac{dx}{dt} \right)=\frac{dx}{dt}(1,2x)$$
(do you recognize implicit differentiation? )We know that the speed is \(5\), and that
$$ \displaystyle v=||\vec{v}||=\left| \frac{dx}{dt} \right|\sqrt{1+{{(2x)}^{2}}}=5$$
This implies that
$$ \displaystyle \frac{dx}{dt}=\frac{5}{\sqrt{1+{{(2x)}^{2}}}}=(\text{at point (1,1)})=\sqrt{5}$$
Therefore,
$$ \displaystyle \vec{v}=\frac{dx}{dt}(1,2x)=\sqrt{5}(1,2)$$
NB: Keep in mind that the \(dx/dt\) term is not a vector, it’s a scalar.
Rules for Differentiation
They work in a similar way as in single variable calculus. There won’t be any nasty expressions, even if dot/cross product is involved. A word of warning: differentiation of vector functions only works if the basis vectors do not depend on the variable of differentiation. An example of the product rule with cross product: \(\displaystyle \frac{d}{dt}(\vec{u}\times \vec{v})=\vec{u}’\vec{v}+\vec{u}\vec{v}’\).
Arc Length
After a minute of though, we quickly realize that the arc length is given by
$$ \displaystyle s=\int_{a}^{b}{\left| \frac{d\vec{r}}{dt} \right|dt=\int_{a}^{b}{|\vec{v}(t)|dt}}=\int_{a}^{b}{v(t)dt}$$
We might recall that when dealing with arc length of functions of one variable, the arc element (do you see the connection between the surface element?) happens to be \(\displaystyle ds=\sqrt{1+{{\left( \frac{dy}{dx} \right)}^{2}}}dx\), which we can obtain by rearranging \(\displaystyle {{(ds)}^{2}}={{(dx)}^{2}}+{{(dy)}^{2}}\) (Pythagoras’s theorem).
Functions of Several Variables
Before we move on to to 3 space, let’s look at one way we can get an understanding for 3 space using 2 space.
Level Curves
Suppose you are walking in a forest and have a map at your disposal. Even if the map is two dimensional, you are still able to apply it to the thee dimensional world. When you see a mountain, it is going to be expressed as a series of circles that indicate the “height”. The same can be done for functions of two variables. Say we have a paraboloid \(\displaystyle {{z}}={{x}^{2}}+{{y}^{2}}\). To find the level curves, we replace \(z\) with a constant \(c\), i.e. \(\displaystyle c={{x}^{2}}+{{y}^{2}}\). Now, this should be quite familiar to many, as it is the equation of a circle. By changing the \(c\), we are actually changing the radius of the circle.
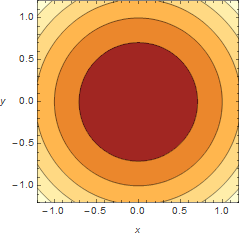
Contour plot
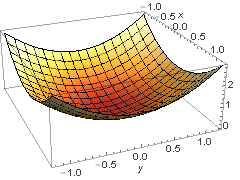
The 3d representation
It’s difficult to get a picture of the 4d world, but at least, using the same principle, it should be possible to gain an understanding.
Derivatives (Vector Calculus)
In Multi Variable Calculus, there isn’t just one operator that we can refer to as derivative. There are three of them:
- grad – \(\displaystyle \nabla f(x,y,z)=\left( {\frac{{\partial f}}{{\partial x}},\frac{{\partial f}}{{\partial y}},\frac{{\partial f}}{{\partial z}}} \right)\qquad \mathbb{R}\to {{\mathbb{R}}^{3}}\)
- div – \(\displaystyle \nabla \cdot \vec{F}=\frac{{\partial f}}{{\partial x}}+\frac{{\partial f}}{{\partial y}}+\frac{{\partial f}}{{\partial z}}\qquad {{\mathbb{R}}^{3}}\to \mathbb{R}\)
- curl – \(\displaystyle \nabla \times \vec{F}=\left( {\begin{array}{*{20}{c}} {\vec{i}} & {\vec{j}} & {\vec{k}} \\ {\frac{\partial }{{\partial x}}} & {\frac{\partial }{{\partial y}}} & {\frac{\partial }{{\partial z}}} \\ {{{F}_{1}}} & {{{F}_{2}}} & {{{F}_{3}}} \end{array}} \right)\qquad {{\mathbb{R}}^{3}}\to {{\mathbb{R}}^{3}}\)
I think we might conclude that all of them use the same symbol (nabla). It’s quite interesting to point out that a lot of information is stored in the notation used. (ToK: Discuss the importance of conveying knowledge through notation)
Gradient
A gradient vector of a function is the normal vector of the function. The norm of a gradient vector tells the maximum rate of increase. The function at \((a,b)\) increases most rapidly in the direction of the gradient vector at point \((a,b)\).
Divergence
Divergence is a measure of the rate at which the field diverges, i.e. spreads away from a point \(p\). I’ve observed that the net total flux of a solenoidal vector field ( \(div \vec F =0\)) is zero. This can be proved by a converting the flux integral into a triple integral using Divergence (Gauss) theorem.
Curl
Curl (rot in Swedish) is a measure of rotation, or differently phrased, how much a vector field swirls around a point.
Identities
Get ready, this will be a long list:
$$ \displaystyle \begin{array}{l}\nabla (\phi \psi )=\phi \nabla \psi +\psi \nabla \phi \\\nabla \cdot (\phi \vec{F})=(\nabla \phi )\cdot \vec{F}+\phi (\nabla \cdot \vec{F})\\\nabla \times (\phi \vec{F})=(\nabla \phi )\times \vec{F}+\phi (\nabla \times \vec{F})\\\nabla \cdot (\vec{F}\times \vec{G})=(\nabla \times \vec{F})\cdot \vec{G}-\vec{F}(\nabla \times \vec{G})\\\nabla \times (\vec{F}\times \vec{G})=(\nabla \cdot \vec{G})\vec{F}+(\vec{G}\cdot \nabla )\vec{F}-(\nabla \cdot \vec{F})\vec{G}-(\vec{F}\cdot \nabla )\vec{G}\\\nabla (\vec{F}\cdot \vec{G})=\vec{F}\times (\nabla \times \vec{G})+\vec{F}\times (\vec{G}\times \nabla )+(\nabla \cdot \vec{F})\vec{G}-(\vec{G}\cdot \nabla )\vec{F}\\\nabla \cdot (\nabla \times \vec{F})=\operatorname{div}curl\\\end{array}$$
Sometimes, it’s clear that they follow the same pattern as the usual product rule in single variable calculus. Some have to be derived brute force. Great that we don’t need to do it and instead can use them to build on top of this knowledge!
Directional Derivative
By looking at the gradient, we might have realized that a normal to surface is no longer a line (as is the case in single variable calculus), but rather a plane, or even a body of some sort. For functions with one variable, we only have one \(\displaystyle \frac{dy}{dx}\), while the gradient contains three “derivatives”, \(\displaystyle \left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \right)\).
Now, back to directional derivatives. Really what it means is the rate of change of \(f(x,y)\) at \((a,b)\) in the direction of a vector \(\vec u\). It’s obtained by:
$$\displaystyle \frac{{\vec{u}}}{||u||}\nabla f(a,b)$$
The cool thing is that, in contrast to the gradient, the directional derivative actually gives us a value rather than a vector (set of values). Since the gradient points in the direction of the maximal increase, it can be useful to set it to be \(\vec u\).
Keep in mind that \(\vec u\) has to be a unit vector, otherwise, we will solve a different problem, namely, the rate of change of \(f(x,y)\) at \((a,b)\) as measured by a moving observer (through \((a,b)\)) with a velocity \(\vec v\).
Taylor Polynomials
From single variable calculus, most of us will recognize Taylor series/polynomials. It’s a way to approximate functions close to a point by a polynomial. It’s quite similar to linearization where we could use the information we have about the slope and the function value in one point to predict the points in its neighborhood. By the way, in MVC, linearization formula looks like:
$$ \displaystyle f(x,y)\approx L(x,y)=f(a,b)+{{f}_{1}}(a,b)(x-a)+{{f}_{2}}(a,b)(y-b)$$
Since we don’t really have the concept of a tangent line, we have a tangent plane instead (the gradient is a set of derivatives, not just one). That’s why we have one \(f\) with subscript 1 and another with subscript 2. Don’t get confused by my notation; the subscript indicates the index of the variable of integration, i.e. \(\displaystyle {{f}_{1}}={{f}_{x}}\).
The general Taylor polynomial is given by
$$ \displaystyle f(\vec{a}+\vec{h})=\sum\limits_{{i=0}}^{m}{{\frac{{{{{(h\cdot \nabla )}}^{j}}f(\vec{a})}}{{j!}}}}+\frac{{{{{(h\cdot \nabla )}}^{{(m+1)}}}f(\vec{a}+\theta \vec{h})}}{{(m+1)!}}$$
or equivalently,
$$ \displaystyle f(\vec{a}+\vec{h})=f(\vec{a})+h\cdot \nabla f(\vec{a})+\frac{{{{{(h\cdot \nabla )}}^{2}}f(\vec{a})}}{{2!}}+\ldots +\frac{{{{{(h\cdot \nabla )}}^{m}}f(\vec{a})}}{{m!}}+\frac{{{{{(h\cdot \nabla )}}^{{m+1}}}f(\vec{a}+\theta \vec{h})}}{{(m+1)!}}$$
The questions I’ve been working with rarely required a polynomial of the third degree (if at all). Assuming that this will be the case during the exam, there’s a neat formula to remeber the the second order Taylor polynomial using a Hessian matrix (will describe under Extreme Value), namely,
$$ \displaystyle f(\vec{a}+\vec{h})=f(\vec{a})+h\cdot \nabla f(\vec{a})+\frac{1}{{2!}}{{\vec{h}}^{T}}\mathbf{H}\vec{h}$$
Exteme Values
Gradient(1st derivative test)
Gradient is a way to find the critical points of a function that occur at \(\displaystyle \nabla g(x,y)=0\).
Hessian (2nd derivative test)
The Hessian matrix is a way to find whether a point is a maximum, minimum or a saddle point. There are four cases:
- Positive definite -> local minimum
- Negative definite -> local maximum
- Indefinite -> saddle point
- Other -> can’t tell.
Lagrange Multipliers
This might sound complex, but it’s all really about finding a maximum or minimum value of a function subjected to a constraint. There are two ways to think about it. In both ways, let \(f(x,b)\) be a function subjected to the constrain \(g(x,y)=0\). Then, we can work with a different function, that is, the Lagrange function: \(\displaystyle L(x,y,z)=f(x,y)+\lambda g(x,y)\) and attempt to find its critical points. The way I think is better is to think about it though is by considering the fact that we want the gradient of the function to be parallel to the gradient of the constraint, i.e. \(\displaystyle \nabla f(x,y)=\lambda \nabla g(x,y)\). Then, we simply need to solve the system of linear equations.
Integrals
In high school, many of us have been taught how to solve $$\int {f(x)dx} $$
Some of the techniques that might ring a bell are partial fractions, substitutions, etc. It might have been mentioned that integration is a way to find the area (depending on the definition) under the graph of a function \(f(x)\). When I confronted MVC, I start to ask myself what each integral really represents, because it’s no longer possible to simply try to evaluate an integral.
Simple Integrals
By simple integrals, I mean \(\displaystyle \iint\limits_{D}{{f(x,y)dA}}\) or \(\displaystyle \iiint\limits_{D}{{f(x,y,z)dV}}\). Here’s an interesting thing that can be observed. \(\displaystyle \int\limits_{D}{{dx}}\) is the length of the domain (a unit length), \(\displaystyle \iint\limits_{D}{{dxdy}}\) represents the area of the domin (squared units), and finally \(\displaystyle \iiint\limits_{D}{{dxdydz}}\) represents the volume of the domain (cube units). If we multiply by a function (inside the integral), we shift the definitions. Instead, the single integral will represent an area, the double integral will be a volume and the triple integral will be ….? Yeah, now we get into things that are quite hard to visualize. Basically, we would get a hyper volume.
Solving Simple Integrals
To solve simple integrals, we can, in most cases, use iteration. I’m not going to get into details, but basically, it’s a way to turn a double/triple integral into single integrals. However, at certain points, the domain we get might be very complicated. As an example, here’s a really simple iteration:
$$ \displaystyle \iint\limits_{\begin{smallmatrix}
0\le x\le 1 \\
0\le y\le 2
\end{smallmatrix}}{{xydxdy=\int\limits_{0}^{2}{{ydy\int\limits_{0}^{1}{{xdx=\{something\}}}}}}}$$
But, suppose we have a different case:
$$ \displaystyle \iint\limits_{{{{x}^{2}}+{{y}^{2}}\le 1}}{{{{x}^{2}}dxdy}}$$
This is not as obvious. However, we can perform a substitution (polar coordinates) to get \(\displaystyle \iint\limits_{{{{x}^{2}}+{{y}^{2}}\le 1}}{{{{x}^{2}}dxdy}}=\int\limits_{0}^{{2\pi }}{{\int\limits_{0}^{1}{{{{r}^{2}}{{{\cos }}^{2}}\theta drd\theta }}}}\). Then, it’s quite easy to find the value. The important conclusion is that \(\displaystyle dA=dxdy=rdrd\theta\). We can find the area/volume element by inserting into a Jacobian matrix, \(\displaystyle \frac{{\partial (x,y)}}{{\partial (r,\theta )}}\).
Advanced Integrals?
The title is, to some extent, misleading, as the integrals aren’t that difficult but it might be harder to conceptualize them. All of the integrals I’m going to describe require understanding of vector fields, which will be described shortly below.
Fields and Integrals
This is the continuation of the previous section with focus on “advanced integrals”.
Fields
My understanding of fields is as a way to describe motion. We can, for instance, have a velocity field, which describes velocity at any given point. So, you give me a location and I will tell you the direction of the velocity vector at that point. In order to illustrate vector fields, we can try to find the field lines. Here’s how:
$$ \displaystyle \frac{{dx}}{{{{F}_{1}}(x,y,z)}}=\frac{{dy}}{{{{F}_{2}}(x,y,z)}}=\frac{{dz}}{{{{F}_{3}}(x,y,z)}}$$
The subscript, in this case, does not denote the partial derivative but rather the component of the vector field. By solving this differential equation, we are able to express the the field lines. For example, if the velocity field is \(\displaystyle \vec{v}=(-y,x)\), we would get \(\displaystyle \frac{{dx}}{{-y}}=\frac{{dy}}{x}\quad \Rightarrow \quad {{x}^{2}}+{{y}^{2}}=c\). Thus, the field lines will look like circles.
In addition, it’s important to keep in mind that there are both scalar fields and vector fields.
Physics and Fields
When I started to study this particular section, I thought it was great that I took physics higher level in high school. Concepts such as conservative fields, equipotential surfaces, etc., made more sense because of the prior knowledge. The cool thing about conservative fields occurs when we want to find the value of a line integral (described later). Since the definition of a conservative field that has the property \(\displaystyle \vec{F}=\nabla \phi \), we can make an attempt to find the potential function \(\phi\) instead and insert the desired starting and ending point. In conclusion, the conservative fields lead to path independence, i.e. it does not matter how we arrive at the end point.
Line Integrals
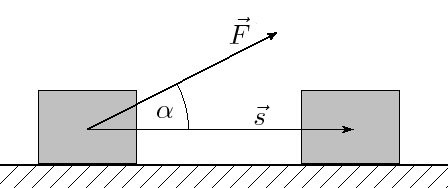
Line integrals are pretty much based on the idea of finding the work (in physics). As we all know, work=force*distance. But, it’s only the x component we need, thus, \(\displaystyle dW=|\vec{F}|\cos \theta ds\). This is the same as \(\displaystyle dW=\vec{F}\cdot \hat{T}ds\). We know from single variable calculus that the tangent points in the direction of the derivative, so, \(\displaystyle \hat{T}=\frac{{d\vec{r}}}{{ds}}\). Integrating this, we get: \(\displaystyle \int\limits_{C}{{\vec{F}\cdot d\vec{r}}}\).
A good strategy is to parametrize the curve when evaluating a line integral.
Surface Integrals
Surface integrals are a step further than a line integral, analogous to the double integral that is a step further than a single integral.
$$ \displaystyle \iint\limits_{S}{fdS=}\iint\limits_{S}{f(\vec{r}(u,v))\left| \frac{\partial \vec{r}}{\partial u}\times \frac{\partial \vec{r}}{\partial u} \right|dudv=}\iint\limits_{S}{f(\vec{r}(u,v))\left| \frac{\partial (x,y,z)}{\partial (u,v)} \right|dudv}$$
As they are not quite the same as double integrals, we have to add a “term”, which can be though of as a conversion factor. In a double integral, we can think of the procedure as adding small rectangles and when we deal with surface integrals, we are essentially attempting the same thing, but a surface can be tilted and bent. So, we are projecting the it onto the \(xy\) plane for instance. There’s going to be a slight difference between the area of the rectangle and the area of the surface, which we compensate using the conversion factor.
Flux Integrals
One of the parts of physics in high school that I found quite hard was flux. However, it’s not really that hard after a half a year of work! A flux integral is essentially a surface integral with some additional terms. Imagine we have a field and we put a surface of some kind in front of that field. If we put it perpendicular to the field (the normal of the surface will be parallel), everything will pass through. In contrast, if the surface is parallel to the surface (the normal vector is perpendicular), nothing will get through. We can relate to the dot product that exhibits similar properties \(\displaystyle a\cdot b=0\quad \Leftrightarrow \quad a\bot b\). Below is a flux integral:
$$ \displaystyle \begin{array}{l}\iint\limits_{S}{\vec{F}\cdot \hat{N}dS=}\iint\limits_{S}{\vec{F}\cdot \left| \frac{\partial (x,y,z)}{\partial (u,v)} \right|dudv}\\\end{array}$$
Connecting Integrals
There are three important theorems in multi variable calculus that connect different kinds of integrals: Green’s theorem, Divergence theorem, and finally Stokes’s theorem.
Green’s Theorem (line = double)
If we have a closed curve, we are able to convert a line integral into a double integral and vice versa, i.e.
$$ \displaystyle \oint\limits_{C}{\vec F\cdot d\vec{r}=\iint\limits_{R}{\left( \frac{\partial {{{\vec{F}}}_{2}}}{\partial x}-\frac{\partial {{{\vec{F}}}_{1}}}{\partial y} \right)}}dA$$
Divergence (Gauss) Theorem (surface = tripple)
If we have a closed surface with a unit normal vector \(\hat N\), we are able to go from a surface integral to a triple (simple) integral, and vice versa.
$$ \displaystyle \iiint\limits_{D}{div\vec{F}dV=\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_C
\vec{F}\cdot \hat{N}dS }$$
Stokes’s Theorem (line = surface)
It’s a way to convert a line integral into a surface integral and vice versa.
$$ \displaystyle \oint\limits_{C}{\vec{F}\cdot d\vec{r}=\iint\limits_{R}{curl\vec{F}\cdot \hat{N}dS}}$$
Physics Applications (other applications)
Apart from those already mentioned, triple integrals can for instance be used to find the center of mass and the mass, i.e.
- The x coordinate of the center of mas is given by \(\frac{\iiint_D x dV}{\iiint_D dV}\)
- The density function \(\rho\) can be integrated to get the mass \(\iiint_D\rho(x,y,z) dV\)
We might ask why we need functions of several variables. Well, the world has many relations where one value depends on several variables. For example, Finance. For example, Riksbanken probably has a mathematical model (I really hope!) of the way interest should be calculated, which can depend on both the interest in European counties, price of houses, etc. There are many variables, which will lead to situations where MVC knowledge will be useful.
Conclusion
I must say that each time I complete a course in mathematics, I get a new picture of the world. In the case of MVC, the great thing in my mind is the combination of single variable calculus and linear algebra (and of course, Physics). I guess it’s like philosophy, it makes you think in different ways.
Release notes for SKGL Extension (2.0.5)
Development of our new Web API is going quite fast. Therefore, it is important to keep SKGL Extension up-to-date so that you can take an advantage of all new features! Today, I want to mention some of the changes that were added to SKGL Extension since 2.0.4.
Changes
- Get Activated Machines is a new method in the Web API (see here) that allows you to get all the activated devices (machine code, IP and Time) for any given key. Note, you need to explicitly enable it as well as use your privateKey for each request. This method has the same authentication level as key generation. An example is shown below:
[TestMethod] public void GetActivatedMachinesTest() { var productVal = SKGL.SKM.LoadProductVariablesFromString("{\"uid\":\"2\",\"pid\":\"3\",\"hsum\":\"751963\"}"); Assert.IsNull(SKGL.SKM.GetActivatedMachines(productVal, "dawdwadwa", "MJAWL-ITPVZ-LKGAN-DLJDN")); var devices = SKGL.SKM.GetActivatedMachines(productVal, "8dOtQ44PdMLPLNzelOtPqVGdrQEVs36Z7aDQEKzJvt8pGYvtPx", "MJAWL-ITPVZ-LKGAN-DLJDN"); }As you can see, in contrast to the classical operations such as validation and activation, pid, uid and hsum are passed in as a JSON array. I hope that all methods will work that way as soon as possible, because it is very easy to simply copy and paste from here and click on “Get C# friendly version”.
- Load and Save Key Information to File will from now on take care of all error handling. This means that you need not to surround these method calls with a try-catch-finally. It’s great because you don’t need to worry if the stream is open during an exception.
Release notes for SKGL Extension (2.0.4)
I am happy to tell all users of SKGL Extension that there is a new version available (since the update in late January). In this post, I would like to mention some changes made to the API, a short usage tip, and then let you know how it is going to change in future.
Changes
- Ability to sign pid, uid, activation date: Based on user feedback, the Web API now allows pid, uid and hsum to be added into the signature. This is particularly important for users that protect more than one product. Before, it was possible to use the same KeyInformation file (serialized by SaveKeyInformationToFile) to unlock other products (that used the same Public Key, i.e. by the same software vendor). For some, it worked out by specifying this information in the Notes field. This change makes it more simple. The activation date is intended for offline key validation; it’s a way to keep track the date of the last activation in order to force the user to activate the software periodically.
- Deactivation: There is a new method that allows you to deactivate a license key. (method info, web api)
- Optional Field: Finally you can access the optional field using .NET. It’s a new type of method that takes in a ProductVariables object instead of separate strings for pid, uid, hsum, etc. Read more below Future ideas (more info).
- Machine code fix: The getEightDigitsLongHash was modified to fix a bug that generated nine digits instead of eight. Read more here.
- Proxy: Get Parameters method allows you to specify the proxy settings.
- Load Product Variables: A new method, LoadProductVariablesFromString allows you to load a serialized version of the ProductVariables object. Read more below Future ideas.
Usage tip
Some users have encountered problems when validating/activating keys because of a wrong code snippet (NullReferenceException). Basically, you should not check the .IsValid field as way to deduce whether the key is valid or invalid. Instead, check if the KeyInformation object is null.
SKGL.KeyInformation keyInfo = new SKGL.KeyInformation();
string machineID = SKGL.SKM.getMachineCode(SKGL.SKM.getSHA1);
keyInfo = SKGL.SKM.KeyActivation("pid", "uid", "hsum", "serialkey", "machine code");
if (keyInfo != null)
{
//valid key
}
else
{
//invalid key
}
Future ideas
As new functionality is added to the Web API, more parameters have to be added to each method. In the long run, this is bad because it can be quite repetitive/confusing to add all the parameters all over again. My plan on how this can be resolved is by adding specialized classes, such as ProductVariables to facilitate reuse of existing variables in other methods. The goal is to make it as easy as possible to use SKGL Extension.
The Beauty of Linear Algebra – Summary
For almost a period I’ve had intense Linear Algebra (some days 4-6 hours), a subject that does not need that much prior learning to be able to understand. You need to know addition and multiplication, that’s it. Yet, the power of linear algebra in real world problems (and highly theoretical problems) is great. The aim of this post is to give a short overview of the subject, summarizing basic concepts.
Introduction
To translate problems into matrix equations can be quite useful. It can allows us to perform simple things as balancing chemical equations (use of Ax=b), take derivatives of polynomials, approximate solutions to overdetermined systems, rotate objects in any space, find volumes, interpret shapes, and so much more. If we think about the very basic concept – matrix multiplication – we simply follow certain rules (a definition) to find the answer. It is quite interesting that we can use this fact to “store” information in matrices, that is, a certain set of actions that have to be performed given a rule. An example of this is differentiation of polynomials (see the ToK marked with blue). Below, I’ve included some examples I constructed using MATLAB.
- Derivative of a polynomial
- Expressing a function with only powers of two
- Multiplying a polynomial by another polynomial
Euclidean Vector Spaces
Since this is simply a subset of General Vector Space and Inner Product Spaces, the interested reader is advised to read those sections instead.
General Vector Spaces
In this section we were introduced to the concept of vector spaces; basically generalizing euclidean vector spaces (3d). Below, some of the questions and focuses:
- How do we find the shortest distance between two lines in n space? Answer, shortest distance is the perpendicular one (by Pythagoras thm). When I am concerned with such problems, I simply pick a general point on the lines, find the line that goes through these points (this expression will contain both \(s\) and \(t\)), and use the power of calculus to find the shortest distance. Note, the calculus approach requires knowledge of multivariable calculus. Otherwise, remember that when dot product is zero, vectors are perpendicular (by definition).
- What is a vector space? It might come as a surprise, but vector spaces are not only about vectors. We can have a polynomial vector space, matrix vector space, etc. The good thing here is that if we can prove that “something” is a vector space, then we are able to apply theorems for general vector spaces on these “something” vector spaces. We should prove that a) closed under addition (\(\vec{u},\vec{v} \in V \implies (\vec{(u+v)}\in V)\ \)), i.e. by adding vectors we never leave the vector space V, and b) that it is closed under scalar multiplication, (\(\vec{v}\in V \implies k\vec{v}\in V, k \in \mathbb{R}\)). A trick is to set the scalar to zero to show that something isn’t a vector space. Lastly, the beautiful thing about mathematics is that many times it’s all about definitions. If I want, I can come up with addition that behaves as multiplication, etc. It’s up to you to decide (we will later see in Inner product spaces that we can define the “dot” product also).
- A subspace? As the name suggests, it’s a vector space that is inside another vector space. Same applies to these also; they should be closed under addition and scalar multiplication.
- Linear dependent/independent? This is all about being able to express a vector as a linear combination of other vectors. If no vector in a vector space \(V\) is expressible as a linear combination of other vectors in \(V\), then these vectors are linearly independent. Ex. If a vector space is spanned by vectors \(\{v_1,v_2,v_3\}\), then if we are unable to express these vectors in terms of each other, they are said to be linearly independent. Otherwise, they are linearly dependent. Recall cross product. We used it in “normal 3d space” (or more academically, orthonormal system with 3 basis vectors) to find a vector that is perpendicular to both vectors. NOTE: Linear independent vectors don’t need to be perpendicular, which is the case with cross product.
- Basis? Above, we saw the use of basis without a proper definition. Not good. Basically, a basis is what makes up a vector space. It’s a set of vectors that are required to be a) linearly independent and b) they should span V (all vectors in V should be expressible as a linear combination of the basis vectors). To test if a basis is linearly independent, simply thrown them in into a matrix (in any direction), and evaluate the determinant. If it isn’t equal to zero, the vectors are said to be linearly independent.
- Column space/row space/null space? Ok, we are getting into highly theoretical grounds (at least at this stage, it might seem so). Given \(A\) is \(m\times n\) matrix. Column space is the subspace of \(\mathbb{R^m}\) that is spanned by the column vectors of \(A\). The row space, as the name suggests, is the sub space of \(\mathbb{R^n}\) that is spanned by the row vectors of \(A\). The null space is the solution space (recurring definition) of \(Ax=0\). A great theorem states that a system of linear equations \(Ax=b\) is consistent if and only if \(b\) is in the column space of \(A\) (\(b\) is expressible as a linear combination of column vectors of \(A\)). “The proof is similar to [..] and is left as an exercise to the reader“(book).
- Theorems? Yes, it turns out that there is a formula that relates the dimension of the column space (\(rank(A)\)) and the dimension of the null space (\(nullity(A)\)). For a matrix with \(n\) columns, we have that \( rank(A)+nullity(A)=n\). I would like to point out that dimension of the column space is equal to the dimension of the row space.
- Orthogonal complements? A good relationship exists between the row space and the null space, and that is that they are orthogonal complements of each other. Orthogonal is a fancy way of saying perpendicular.
- Is it possible to change basis vectors? Yes, this is perfectly fine. We use a matrix \(T\) that will function as a converter (ToK: Discuss the importance of representing of a set of instructions in a more abstract form). Here’s the relationship, $$(\vec{v})_{B’}= {}_{B’}{T_B}(\vec{v})_{B})$$If we know the basis vectors of \(B’\) and \(B\), we can get the transition matrix by putting the basis vectors as columns in \([B’|B]\) and perform elementary row operations until we get to \([I|{}_{B’}{T_B}]\). In general, $$[new|old]\sim \text{el. row op.}\sim [I|old\to new]$$
- How does the notion of functions apply to vector spaces? From high school, many of us should be familiar with the fact that a function maps one value to another value. This can be applied to vector spaces. Again, it’s always good to have a solid definition. We say that \(T:V\to W\) is a function from vector space V to W, then T is a linear transformation if the following criteria is fulfilled: a) \(T(k\vec{v})=kT(\vec{v})\) and b) \(T(\vec{u}+\vec{v}) = T(\vec{u})+T(\vec{v})\). The good thing about being able to transform from one vector to another is that when this is put into a computer, we can do all sorts of cool things. For example, we can reflect, project, and rotate objects. We can also contract and dilate vectors, and this can be expressed in matrix form. Sometimes, we might want to perform two things at once, reflect and rotate maybe, then, we simply multiply the transformation matrices together in this order: rotate*reflect. Always think from right to left.
Inner Product Spaces
The fact that it is possible to generalize the notion of vector spaces suggests that the same can be done for operations that are performed inside a vector space.
- What is an Inner product space (real vector space)? By definition, this is a vector space where we have an inner product with following properties.
- \(<\vec{u}|\vec{v}>=<\vec{v}|\vec{u}>\)
- \(<\vec{u}|\lambda\vec{v}>=\lambda <\vec{u}|\vec{v}>\)
- \(<\vec{u}|\vec{v} +\vec{w}>= <\vec{u}|\vec{v}> <\vec{u}|\vec{w}>\)
- \(<\vec{u}|\vec{u}> \ge 0\) and \(<\vec{u}|\vec{u}> = 0 \iff \vec{u}=0\)
This is essentially the dot product in \(\mathbb{R^n}\). The good thing about generalizing it is that “something” does not necessarily need to be in \(\mathbb{R^n}\) to be an inner product space. For example, we can have an inner product space of all continuous functions (denoted by \(C[a,b]\)). Then, the inner product is defined as: $$<f(t)|g(t)>\int_a^b f(t)g(t)dt$$Since polynomials are continuous functions, this definition applies to polynomial inner product spaces.
- What is perpendicularity (orthogonality)? In a a vector space with an inner product \( <\vec{u}|\vec{v}>\), the angle between \( \vec{u}\) and \( \vec{v}\) is defined as $$cos \theta = \frac{{ < \vec u|\vec v > }}{{||u||||v||}}$$Cauchy-Schwarz identity is quite useful and is given by: \(<\vec{u}|\vec{v}>^2\le ||\vec{u}||^2||\vec{v}||^2\)
- How to project a vector on a subspace of an inner product space? Since we have a generalized version of the dot product, it’s possible to generalize the projection of a vector on a subspace. Here’s how: Given an orthogonal (this is crucial) basis for \(W\in V\), say \(\{ {{\vec v}_1} \ldots {{\vec v}_n}\} \) and that \(\vec{u} \in V \), then: $${{\mathop{\rm Proj}\nolimits} _W}\vec u = \frac{{ < \vec u|{{\vec v}_1} > }}{{||{{\vec v}_1}|{|^2}}}{{\vec v}_1} + \ldots + \frac{{ < \vec u|{{\vec v}_n} > }}{{||{{\vec v}_n}|{|^2}}}{{\vec v}_n}$$
- How to find an orthogonal basis? Note that the projection on “formula” only works if the basis is orthogonal. In order to find an orthogonal basis, we can use Gram-Schmidt process.$$\begin{array}{l}
{\rm{Step 1: }}{{\vec v}_1} = {{\vec u}_1}\\
{\rm{Step 2: }}{{\vec v}_2} = {{\vec u}_2} – \frac{{ < {{\vec u}_2}|{v_1} > }}{{||{{\vec v}_1}|{|^2}}}{{\vec v}_1}\\
{\rm{Step 3: }}{{\vec v}_3} = {u_3} – \frac{{ < {{\vec u}_3}|{{\vec v}_1} > }}{{||{{\vec v}_1}|{|^2}}}{{\vec v}_1} – \frac{{ < {{\vec u}_3}|{{\vec v}_2} > }}{{||{{\vec v}_2}||}}{{\vec v}_2}\\
\vdots \\
{\text{r times}}
\end{array}$$ Remember that $$ \vec u = {{\mathop{\rm Proj}\nolimits} _W}\vec u + {{\mathop{\rm Proj}\nolimits} _{{W^{\bot}}}}\vec{u}$$ - How to find the “best” solution in an over-determined system? A good approach is to apply Least Square method. Over-determined systems occur in scientific measurements, and so if the error is assumed to be normally distributed, we can use the method of Least Squares. The idea is to think about the system’s column space and then try to project the measurements on the plane that the column space spans. It turns out that the best solution is $$x = {({A^T}A)^{ – 1}}{A^T}b$$ Keep in mind that it’s not required to have an orthogonal basis (i.e. the column space does not have to be orthogonal). Using this, we can express the projection formula as a simple matrix multiplication $${{\mathop{\rm Proj}\nolimits} _L}\vec u = A{({A^T}A)^{ – 1}}{A^T}b$$An interesting property that can be obtained is that \(A^TA\) is invertible if and only if the column space of A is linearly independent.
Linear Transformations
I think the Swedish term linjär avbildning conveys more information rather than just stating linear transformation. The term basically means linear depiction, which is what this topic is about. At the first sight, this might seem as converting from one base to another. This isn’t entirely true, I’ve realized. It’s more appropriate to view this as a function that maps one value to another. As functions can be injective, surjective, bijective, it’s not implied that we should always be able to map a transformed point back to the original point. In contrast, when changing bases, it’s always possible to get from one basis to another; you never really introduce/remove more information.
- How to define Linear Transformation? A linear transformation \(A: V\to W\) should have the following properties:
- \( A(\vec {u} + \vec {v}) = A(\vec {u}) + A(\vec {v}) \)
- \(A(\lambda \vec u) = \lambda A(\vec u)\)
- What is Kernel and Image space(range)? If you’ve read what I wrote in General Vector Spaces, the Kernel = Null space and Image space = Column space.
- Example? Let’s define the following linear transformation $$\begin{array}{l}
A(1,2,0) = (1,1,1)\\
A(0,1,2) = (0,1,1)\\
A(1,3,3) = (0,0,1)
\end{array}$$Unfortunately, this is not so useful if we want to transform a vector with the matrix A. It is easier if we would have the standard basis vectors on the left hand side. So, similar to the change in basis example, we put this into a matrix try to get an identity matrix on the left hand side. This method (Martin’s method) was discovered by Martin Wennerstein 2003. See the formal explanation of the method. - Relation between column space of composite linear transformations? Given that \(B\) has full rank, i.e. \(rank(B)=n\), then \(rank(BA)=rank(A)\). Motivation: This is obvious if we consider the transformation \(BA\) means. First, we perform transformation \(A\), which will lead us to the image of A (\(range(A)\)). That is, all vectors will be depicted on the image space of \(A\). When transformation \(B\) is performed, all vectors in the image space of \(A\) will be transformed using \(B\). Note, \(B\) kernel is trivial, i.e. the zero vector transforms to zero vector.
- What’s special about the kernel? It can be useful to think of kernel as “the information that gets lost during a transformation”(KTH student). For example, if the kernel contains more than just a zero vector (i.e. it’s non-trivial), when we perform a transformation, some vectors will be depicted on the zero vector; thus “information” disappears.
- What is injectivite, surjective, and bijective? Let \(A:V \to W\). Injective (one-to-one) is if \(\vec x \ne \vec x’ \implies A(\vec x) \ne A(\vec x’)\), i.e. each vector is represented by a unique vector (so we can map back to the original vector after a transformation). Surjective (onto) is if \(\forall \vec y \in W\exists \vec x \in V:\vec y = A\vec x\), i.e. for all vectors in the image of \(A\), we can map it to the original vector. Bijective is when it’s both injective and surjective.
- Properties? For something to be injective, the dimension of the kernel has to be zero. For \(A: V\to W\) to be surjective, \(dim ker(A)=dim(W)\). This can be proved by the dimension theorem and the definition of surjectivity.
Eigenvalues
An eigenvalue is the value lambda in \(A\vec x = \lambda \vec x\). It can be, for instance, applied in problems such as a) Find $$ {A^{1000}}\left( \begin{array}{l}
2\\
1
\end{array} \right) $$given that we know A, or b) express \(2x_1^2+ 2x_2^2+2x_3^2+4x_1x_2\) (see this) without the cross product terms. The latter is particularly good when identifying shapes that have been rotated/transformed.
- How to find eigenvalues? Simply solve \( \det (A – \lambda I) = 0\), the characteristic equation.
- How to find the eigenvectors corresponding to eigenvalues? Solve \((A – \lambda I)\vec x = 0\).
- Express a matrix using eigenvalues and eigenvectors? We can always express a matrix A as \(A = PD{P^{ – 1}}\). If P happens to be orthogonal (i.e. the rows/columns space forms an orthonormal base), then we can express it as \( A = PD{P^T}\) because of a property of orthogonal matrices that states that \(A{A^T} = I\) or equivalently that \( {A^{ – 1}} = {A^T}\).
- Raising matrices to a certain power? It can be shown that \({A^k} = P{D^k}{P^{ – 1}}\).
- Applying orthogonal deagonalization on quadratic form? $$\begin{array}{l}
a{x^2} + b{y^2} + c{z^2} + d{x_1}{x_2} + e{x_1}{x_3} + f{x_2}{x_3} = \\
= ({x_1},{x_2},{x_3})\left( {\begin{array}{*{20}{c}}
a&{d/2}&{e/2}\\
{d/2}&b&{f/2}\\
{e/2}&{f/2}&c
\end{array}} \right)\left( \begin{array}{l}
{x_1}\\
{x_2}\\
{x_3}
\end{array} \right)
\end{array}$$Now, this can be seen as \(x^TAx\). If we make a substitution \(\vec x = P\vec y\) such that \(P\) orthogonaly diagonalizes \(A\), then $$ {x^T}Ax = {(P\vec y)^T}A(P\vec y) = {y^T}({P^T}AP)y$$ - Orthogonal matrices? In an orthogonal matrix, the row vectors form an orthonormal base (same for column vectors). An interesting property that exists when multiplying a vector \(x\) is $$||A\vec x||=||\vec x||$$ and $$A\vec x * A \vec y=\vec x* \vec y$$Then, as we mentioned previously, the inverse of an orthogonal matrix is simply the transpose (please see my answer for a possible application).
What’s new in SKGL Extension for .NET (v. 2)
The extension API for SKGL used to communicate with the Web API of Serial Key Manager has now been upgraded to support Web API 2.0. Below, I’ve listed some changes:
- The project was moved to GitHub: You can find it here.
- Some methods were removed/renamed: From now on, there is only one method for a specific action (eg. Activate). There is, for instance, only one method to perform activation, and that method will return a KeyInformation object rather than just stating whether the key is valid or invalid.
- Support for error handling: When something is missing, you will receive an error. All errors are well documented here. In debug mode, these errors will be displayed in the output.
- New hash methods and improved algorithm for data collection: The API uses an improved version of information collection (see all contributors) that is later hashed by a hashing algorithm. There are two algorithms at the movement: one that will calculate an eight digit long hash and a second one that will use SHA1. It’s always possible to pick any other hashing algorithm.
I can imagine that some of the changes may or may not trigger different kinds of emotions, partly because some code has to be modified. However, this upgrade is necessary as it will allow much more functionality to be added in the future. It’s also easier to use and thus make it work on other platforms.
Therefore, I will be available to answer some questions on how to migrate to the new library. I can’t guarantee a fast response time, but I will do my best. To save my time, please look through this page first, before contacting me. BUT first, please consider submitting your question on https://github.com/artemlos/SKGL-Extension-for-dot-NET/issues/new. If you rather prefer CodePlex, please use https://skgl.codeplex.com/discussions/topics/5452/help-support.
Links:
A book for young computer scientist
Today, I published one of my summer projects – a book (a chapter) – as open-source, on GitHub. The reason why it’s open source, the purpose and goal, and finally how I got started is described below.
Why open source?
The initial aim of the book was to make computer science mathematics more accessible, which shaped it quite a lot. First of all, the programming language used is JavaScript, which I believe is the one many people have access to. Not all languages are like that, and some you have to pay for. JavaScript, on the other hand, can be access on all machines (computers, phones) that have access to a web browser. Secondly, the book can, from now on, be accessed free of charge. The code (written in TeX) is also available. I hope that this will allow an even greater audience able to access it. Thirdly, each chapter (right now it’s only one) should describe the subject from scratch. It’s not assumed that you should have some prior knowledge to be able to understand it.
Purpose and goal
I’ve partly described it above, but there is more to it. There are two groups the book should target: young programmers and non-programmers. Regarding the first group, my experience tells me that there is a tendency that many young programmers skip the underlying concepts of mathematics behind some computer operations and instead focus on the code (in some cases, you don’t even need to code that much). The latter group will still find many concepts interesting and my goal is to show that computer science is fun and not as scary as they might think.
How it started
The first time I came across this idea is when I was contacted by an editor at Apress in the beginning of November 2013. Before that, I recently published a short course reference for Algorithms via C# course, which I haven’t had the opportunity to start properly (see KSDN). After a consultation with one of my teachers, I decided to keep focused on the diploma to get good grades and later on the book. So, sometime in June I started writing the chapter about modular arithmetic that I thought I knew a lot of about. But, when I started writing I had to continue doing research and learn the concepts (from several sources) and later write it down. Since I want to write it in my own phase (when I have time) and want people to have access to it, it’s not published as a traditional book but rather as a digital one.
More information
“Trits” instead of “bits” – a short introduction to balanced ternary
It’s usually said that students who would like to study computer science should familiarize themselves with binary representation of numbers and thus get used to very common powers of 2, i.e. 2¹=2, 2²=4, 2³=8, etc. That’s definitely true; the digital world we live in uses bits and almost all programming languages are based on Boolean algebra. But, just because something is popular does not mean it’s good. In this short article, my aim is to give the reader a general understanding of the concept of balanced ternary, the benefits of using it, and finally some history of earlier attempts to create ternary computers.
Intro
The concept Balanced ternary has many underlying ideas, so let’s try to break it down into things we can relate to. The word ternary, in this context, refers to ternary numeral system. A numeral system is a way different people express numbers: the Great Greeks used a superscript on letters to identify numbers, i.e. α’, β’, γ’. In the Roman Empire, they used I, II, III, IV (we still use these numbers in names, i.e. Charles XII). Many people nowadays use numbers like 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (origin from Hindu-Arabic numbers). This way of writing numbers can be referred to as base 10 or simply decimal. A ternary numeral base is similar to decimal, but allows only 0, 1, 2. In binary (base 2), we only allow 0, 1.
| Decimal (Base 10) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ternary (Base 3) | 0 | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 | 101 |
A clear observation from this table is that once digits end (i.e. going from 9 to 10), we put a zero and carry a 1 forward (in the number). This is similar to base 3, however, since we only have 0, 1, 2, our digits end faster than in base 10.
There exists an algorithm to convert between different bases, but that would probably be better suited for another article. Therefore, it’s not going to be discussed here (convert numbers). However, it’s quite simple to convert from base 3 to base 10 by an interesting observation. For example, 123 is equivalent to saying that 123= 1*10²+2*10¹+3*10⁰ = 1*100+2*10+3. In base 3, we have a similar approach, but instead of 10, we use 3. Say we want to convert 22 (in base 3) to base 10. Therefore, 2*3¹+2*3⁰=2*3+2=8 (in base 10). This conclusion goes hand in hand with the one in the table.
Now, we should have some grasp of ternary numeral systems. Let’s move on to the term balanced. A intuitive way of thinking about it that something should be balanced, like masses on opposite sides of a weight should cancel out. So, how would such system look like? I turns out that instead of saying that we can use digits 0, 1, 2 we instead introduce -1 so that the digits in the balanced ternary system are -1, 0, 1 (looks to be balanced?). Let’s refer to the -1 as n and 1 as p. The table below links the numbers in base 10 with the ones in balanced ternary.
| Decimal (Base 10) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Balanced Ternary (Base 3) | 0 | p | pn | p0 | pp | pnn | pn0 | pnp | p0n | p00 | p0p |
There is a similar pattern here as for unbalanced ternary. The interested reader should consider to experiment with this concept by implementing it in the favourite programming language (see all implementations).
Benefits
Here are some of the benefits of the balanced ternary:
- The sign (+/-) is stored in the number, and can be deduced by the leading trit (similar to bit). So, if a number starts with -1, or using our notation, n, we know it’s negative.
- In order to get the number with the opposite sign, simply replace all n‘s with p‘s and all p‘s with n‘s. Eg. Since 7 is pnp, -7 is npn.
- In order to round to the nearest integer, the fractional part should be removed.
- Things don’t have to be either true or false. There exists an unknown case also.
History
It might seem that this idea works in theory but not in real computers. However, this is not true. At Moscow State University, a series of Setun computers was developed. The first Setun was built in 1958. An interesting thing that can be noted is that it used ternary logic.
Further reading
For those who are interested, please take a look at the links below:
- http://www.computer-museum.ru/english/setun.htm
- http://en.wikipedia.org/wiki/Heyting_algebra
- http://tunguska.sourceforge.net/The_Fine_Manual.pdf
Edits:
- Corrected the base10-base3 table.
- First published 20.12.2014 (dd/mm/yyyy)
Keeping Track of Code Quality with NDepend
In the recent lecture at the Computer Science programme, we’ve discussed the way projects should be designed. There are three very important criteria: Coupling, Cohesion and Responsibility driven design. We might question the use of encapsulation, avoidance of code duplication and writing very specialized classes. Some might argue that once we’ve solved a particular task in a limited amount of time, it’s possible to move on and solve other tasks. However, based on my experience from Mathos Project mainly, I can conclude that if the code would be written that way, the project would have collapsed. The reason is, in particular in open source projects, is that it’s not as strictly decided which team writes and maintains a particular module. One developer might contribute with a specific functionality, and another with a different functionality in the same module. Then, we might get a different set of people trying to understand what they’ve done to build on top of it. Even the authors of the code might not be able to understand or “dare to modify” their own code. This phenomena can be referred to as legacy code. In conclusion, we don’t want that to happen!
For some weeks ago, I received a copy of NDepend (Developer edition and Build machine edition) from Patrick Smacchia, the Lead Developer of NDepend. This made me very happy and I started to test it on my current projects. In this article, I am going to explore some of the functionality available in NDepend. Please note that I am just describing features that came first in to my sight. NDepend is a very advanced system and contains a lot more functionality than I’ve mentioned here. Many specialized books have referred to the system and it’s also recommended by for instance Jeffrey Richter (I’ve referred to one of his works in this article) and Scott Hanselman. (For a more complete tutorial, please see this Pluralsight course)
First impression
Once I installed NDepend and test-launched it, I was able to generate a comprehensive report without reading any documentation. It’s a friendly GUI that suggests you what you can do at any point during the code analysis.
Even if it might appear as if it’s so much new information that has to be interpreted, there is a Get Started feature built-in to the report (top, right corner). It suggests that we should look out for unwanted dependencies, look for complex methods, etc. Personally, the first thing that fell into my sight is the percentage of comments in the project. Recently, Mathos Project promoted the idea to write xml comments to each new method as it is implemented. Since all analysis are saved regularly, I could have generated a report before the first post about the xml comment idea and compared it to the recent report. The percentage would tell me if we are moving the right direction. This is good not only from a developer point of view, but a also from a project manager stand point.
Visualization of projects
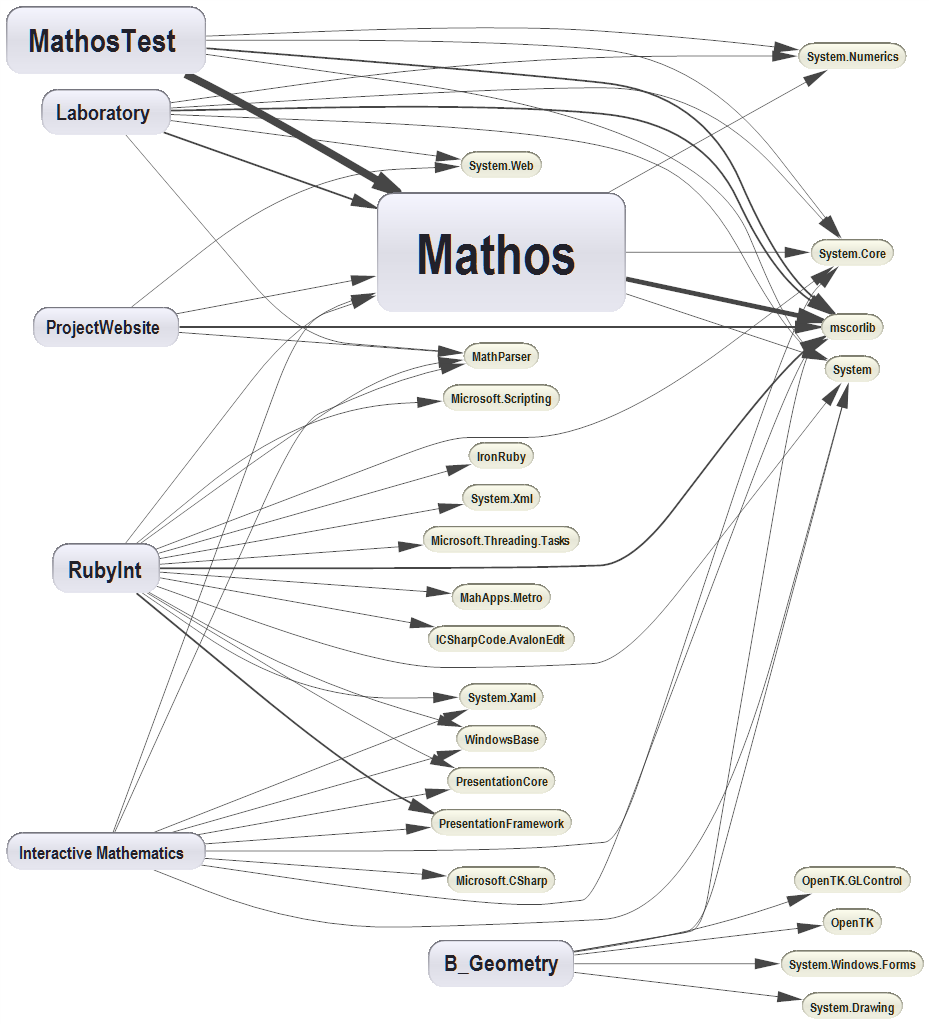
It’s always good to quantify big things into something that can easily be interpreted. NDepend provides you with many kinds of graph by default, but it is also possible to specify your own parameters. Let’s look at the simplest Component Dependency graph below:
Visual Studio Ultimate allows you to generate similar graphs, but in NDepend more information is encoded into the graph. For instance, the number of dependencies is proportional to the size of a project in the diagram. If you open this diagram in NDepend, you will be able to get more information by hovering a box. An example is show below
This is quite good if you want to spot strongly coupled classes. The thicker arrow, the more depended is a class on another class. Moreover, if a more complex analysis should be performed, we can look at code metrics. I am going to analyse complexity in terms of lines of code, but this can adjusted.
Each of these small rectangles represents a method, where the area is proportional to the lines of code that method (we can change this to another property). The rectangles selected in blue are top ten methods that either have too many variables, parameters, or lines of code (read more here). If you spot a method that you want to inspect, simply double click on it and you will be redirected directly into your project where the method is located. This is quite good if we want to spot high or low cohesion. There is a tendency that the simpler a method/class is, the more specialized is the class at a particular task.
Abstractions
In addition to the diagrams I’ve already shown above, one that I really liked (partly because of the simplicity) is the Abstractness vs. Instability graphs. I’ve compared one for Mathos Core Library and Mathos Parser.
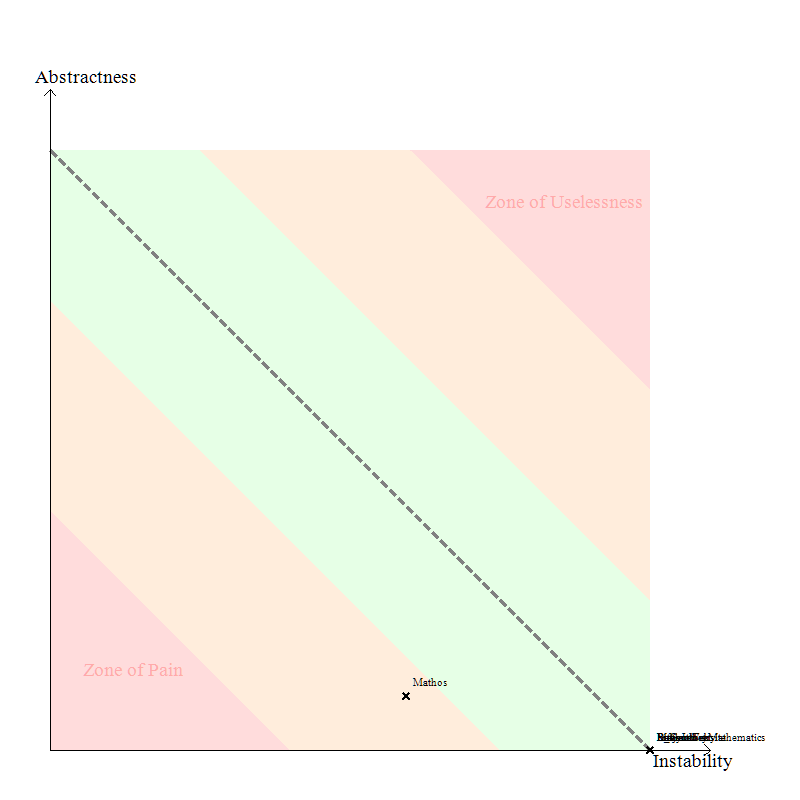
Mathos Core Library
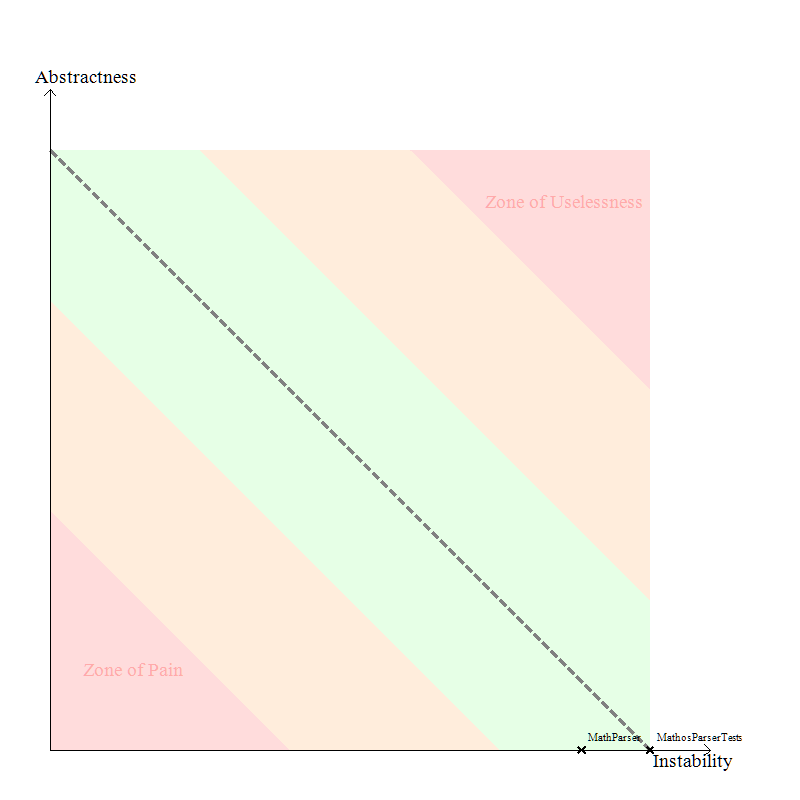
Mathos Parser
Note, Instability is a good thing since Stable means “painful to modify” according to the definition. It seems like Mathos Parser is in the safe zone and Mathos Core Library is close to it.
Creating custom rules
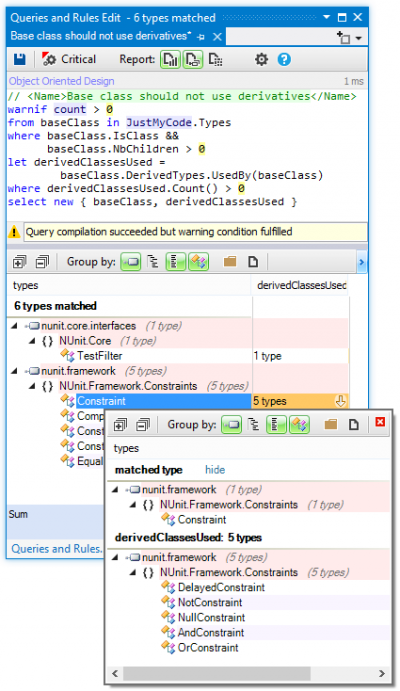
The report I’ve generated used the standard rules (you can see some of them here). It is possible to use the C# Linq to make your own rules. You can find more about how to construct your own rules here. It is quite straight forward. Here is one of the standard rules that measures method complexity:
warnif count > 0 from m in JustMyCode.Methods where
m.ILCyclomaticComplexity > 40 &&
m.ILNestingDepth > 5
orderby m.ILCyclomaticComplexity descending,
m.ILNestingDepth descending
select new { m, m.ILCyclomaticComplexity, m.ILNestingDepth }
An example of this functionality is shown below:
Conclusion
Based on my experience with NDepend, I strongly recommend this system to developers working on projects, particularly large-scale projects. Even if you are not using .NET, I believe it’s a good idea to get some basic knowledge of it. Some weeks ago, the .NET team at Microsoft announced that the .NET Core is going to be open source, which in my opinion will make the .NET framework even more influential in environments like Linux, Mac etc. On your .NET journey, I am quite convinced that NDepend will help you to make good design decisions easier and thus make your project not only good at performing tasks, but also a pleasure to read for new developers!
Edits:
- Published 2014.012.05
- Added a picture of C# Linq overview.