Introduction
Most of the people are certainly familiar with Calculus already from high school and the beginning of university. It is usually associated with concepts like infinitely small, behaviour at infinity, finding the area under the graph, and finding the rate of change. It seems to be so much about infinity (which is difficult to imagine) but not that much about finite values. So why not look at finite differences instead? In this article, we are going to see how powerful the concept difference is, and how we can apply it to real world problems. First, we are going to look at how the difference can be found in a sequence. Secondly, the way we can find the next term and later on how we can get a formula to generate the nth term. Finally, we are going to use the idea of finding the nth term to find an expression of the sum.
The difference operation
It is quite intuitive, once we see a sequence, to try to find the difference between adjacent terms. If we are not satisfied, we look at the difference of the differences, and so on. Our aim now is to construct a method that will behave like we normally would in this situation. First, however, let’s look at what happens when we take the difference of each term.
| \(a_0\) | |||
| \(a_1-a_0\) | |||
| \(a_1\) | \(a_2-2a_1+a_0\) | ||
| \( a_2-a_1\) | \(a_3-3a_2+3a_1-a_0\) | ||
| \(a_2\) | \(a_3-2a_2+a_1\) | ||
| \(a_3-a_2\) | |||
| \(a_3\) |
We can take the difference as many times as we like, but given that a sequence was constructed with only addition, subtraction, multiplication and division i.e. it was a polynomial, there is going to be a point when we can stop taking the difference. The important thing now to realize from this figure is that the difference expression contains the coefficients from the Pascal’s triangle. This is good if we want to take the difference many number of times. The code below utilizes this observation.
/// <summary>
/// Finds the difference between terms in a sequence. By chaging the degree, we can take difference of the differences.
/// </summary>
/// <param name="sequence">The sequence of doubles passed in as a double array.</param>
/// <param name="term">The index of the first term where the diff. should be taken. NB: As the degree increases, the smaller can the term be</param>
/// <param name="degree">The type of difference, i.e. if degree=1, the first difference is taken and if degree=2, the difference of the first difference is taken. </param>
/// <example>If the sequence is {1,2,3,4,...}, term=0, degree=1, we get 1. By changning degree=2, we get 0.</example>
/// <returns>The difference between the terms in the sequence, depending on the degree.</returns>
public static double GetDifference(double[] sequence, int term, int degree)
{
// the pascal's triangle should be optimized. we only need half of the values
double result = 0;
bool evenStart = (term + degree) % 2 == 0 ? true : false;
int j = 0;
for (int i = term + degree; j <= degree; i--)
{
result += Pascal(degree, j) * sequence[i] * (evenStart ? (i % 2 == 0 ? 1 : -1) : (i % 2 == 0 ? -1 : 1));
j++;
}
return result;
}
Finding the next term
Before we proceed in finding the next term and ultimately the polynomial describing the nth term, let’s focus our attention on a real world example. Say we have the sequence \(\{n^2\}\) i.e. \(1, 4, 9, 16 \dots\). We assume that we don’t know the nth term, i.e. we only know some values of the sequence. The common procedure in this case is to look at the differences, similar to the previous section. For example,
| \(1\) | |||
| \(3\) | |||
| \(4\) | \(2\) | ||
| \( 5\) | \(0\) | ||
| \(9\) | \(2\) | ||
| \(7\) | |||
| \(16\) |
To be sure that we’ve found a pattern, we should end up at zero (assuming a polynomial generated the sequence). The interesting thing about this figure is that we know that each difference in the table can be expressed in terms of the difference expressions in the previous section. So, \(3=(4)-(1)\) and \(2 = (9)-2\times (4)+(1)\). This idea hints us to a possible way of finding the next term in the sequence. Since we know that the second difference \(2\) is constant, we can find an expression for the next term by some simple arithmetic. That is, \(2=a_n -2\times a_{n-1} + a_{n-2}\). Thus we can find the nth term given the two terms before it. This is done by the following code:
/// <summary>
/// Finds the next term in the sequence, given that a pattern exist.
/// </summary>
/// <param name="sequence">The sequence of doubles passed in as a double array.</param>
/// <param name="term">If term=-1, the next term in the sequence is going to be found. By default, you don't need to change this variable.</param>
/// <returns></returns>
public static double GetNextTerm(double[] sequence, int term = -1)
{
int constantIndex = 0;
if (HasPattern(sequence, out constantIndex))
{
double constant = GetDifference(sequence, 0, constantIndex - 1);
if (term == -1)
{
// have find the term to start with to figure out the n+1 term.
term = sequence.Length - constantIndex;
}
double result = 0;
bool evenStart = (term + constantIndex - 1) % 2 == 0 ? true : false;
int j = 1;
result += constant;
for (int i = term + constantIndex - 1; j <= constantIndex - 1; i--)
{
result += Pascal(constantIndex - 1, j) * sequence[i] * (evenStart ? (i % 2 == 0 ? 1 : -1) : (i % 2 == 0 ? -1 : 1));
j++;
}
return result;
}
throw new Exception("The sequence does not contain a recognized pattern.");
}
Finding the expression for the nth term
This is a bit more tricky to find in contrast to what we’ve done so far. The nth term is very dependent on the number of times the difference operation has to be taken before we end up at zero. In the previous example, we had to take it three times to get to zero. The polynomial we got had the second degree. It turns out that if we had to take the difference \(n\) times to get to zero, the polynomial is of the degree \(n-1\). This is quite useful, because if we know how the polynomial looks like, the only thing we need to find are the coefficients (more in-depth tutorial).
In the sequence \(1,4,9,16\dots\), we had to take the difference three times, so the polynomial has the second degree, i.e. \(ax^2+bx+c\). We have three unknowns, so we need three data points to solve the system of equations. That is,
\(\left[ {\begin{array}{*{20}{c}} 1 & 1 & 1 & 1 \\ 4 & 2 & 1 & 4 \\ 9 & 3 & 1 & 9 \end{array}} \right]\)
When we reduce this matrix to echelon form, we get that the coefficient for \(n^2 \) is \(1\), and zero for the remaining terms. The code below does this task.
/// <summary>
/// Finds the coefficients of the nth term and returns them in a double array. The first item in the array is of the highest power. The last term in the array is the constant term.
/// </summary>
/// <param name="sequence">The sequence of doubles passed in as a double array.</param>
/// <param name="degree">The degree value returned here is the number of times we have to take the differnce of this sequence (using GetDifference) to get the difference to be zero.</param>
/// <returns></returns>
public static double[] GetCoefficientsForNthTerm(double[] sequence, int degree)
{
var mat = new Matrix(degree, degree + 1);
for (int i = 0; i < degree; i++)
{
for (int j = 0; j <= degree; j++)
{
if (j == degree)
{
mat[i, j] = sequence[i];
}
else
{
mat[i, j] = Get.IntPower(i + 1, (short)(degree - j - 1));
}
}
}
mat.RREF();
var output = new double[degree];
for (int i = 0; i < degree ; i++)
{
output[i] = mat[i, degree];
}
return output;
}
The coefficients we get correspond to a term in the polynomial. For example, if we get \(3, 2, 1\), the polynomial is \(3x^2+2x+1\).
Finding the closed form for the sum
When we first think about how we can find the closed form for a sum, we might conclude that it is difficult. In Concrete Mathematics – A Foundation for Computer Science, an entire chapter (chp. 2) and a great part of other chapters is dedicated to sums, and the way we can find the anti-difference. At least, that was my thought when I got this idea. But later, an interesting thought came up to my mind, and that is to treat the sum as a sequence and the sequence as the difference of the sums’ terms. Let’s clarify this. If we have the sequence \( 1,2,3,4,\dots\), we can construct the partial sums, i.e. \(1, 1+2, 1+3+4, 1+2+3+4\), thus \(1, 3, 6, 10\). But the partial sums form a new sequence which we can analyse in a similar way. This means that can we can reuse quite a lot of code. Now, since in the original sequence \( 1,2,3,4,\dots\), we have to take the difference twice to get zero, in the new sequence \(1, 3, 6, 10\), we have to take the difference three times. The code for doing this is shorter, in contrast to the previous ones.
/// <summary>
/// Finds the coefficients of the closed form of the sum and returns them in a double array. The first item in the array is of the highest power. The last term in the array is the constant term.
/// </summary>
/// <param name="sequence">The sequence of doubles passed in as a double array.</param>
/// <param name="degree">The degree value returned here is the number of times we have to take the differnce of this sequence (using GetDifference) to get the difference to be zero.</param>
/// <returns></returns>
public static double[] GetCoefficientsForNthSum(double[] sequence, int degree)
{
double[] partialSums = new double[sequence.Length];
partialSums[0] = sequence[0];
for (int i = 1; i < sequence.Length; i++)
{
partialSums[i] = partialSums[i - 1] + sequence[i];
}
return GetCoefficientsForNthTerm(partialSums, degree + 1);
}
Limitations
One of the limitations of this code/algorithm is that we can only use sequences that have been generated by a polynomial. Exponents are not allowed, although \(n^2= n\times n\), so that works. The reason is quite simple. Formally, we define difference as an operator on a function (similar to derivatives) as
\(\Delta f(x) = f(x+1) – f(x)\). Let’s say we have \(f(x)=2^x\). If we take \(\Delta(2^x)=2^{x+1}-2^x=2^x(2-1)=2^x\). Not good, no matter how many times we take the difference, we end up with the same thing we had in the beginning. This is why this particular algorithm does not work in this case. It is possible to add an extra step that checks against known sequences each time a difference is taken. This, I will do a bit later! 🙂
Source code
You can find all additional methods in the FiniteCalculus class in Mathos.Calculus (Mathos Core Library). Also, you can see this code in action here!
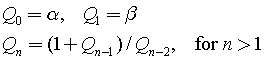
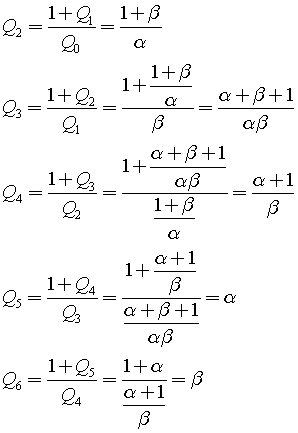
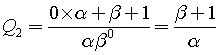
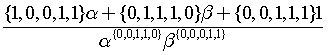 .
.