artemlos
This user hasn't shared any biographical information
Most of the people are certainly familiar with Calculus already from high school and the beginning of university. It is usually associated with concepts like infinitely small, behaviour at infinity, finding the area under the graph, and finding the rate of change. It seems to be so much about infinity (which is difficult to imagine) but not that much about finite values. So why not look at finite differences instead? In this article, we are going to see how powerful the concept difference is, and how we can apply it to real world problems. First, we are going to look at how the difference can be found in a sequence. Secondly, the way we can find the next term and later on how we can get a formula to generate the nth term. Finally, we are going to use the idea of finding the nth term to find an expression of the sum.
It is quite intuitive, once we see a sequence, to try to find the difference between adjacent terms. If we are not satisfied, we look at the difference of the differences, and so on. Our aim now is to construct a method that will behave like we normally would in this situation. First, however, let’s look at what happens when we take the difference of each term.
| \(a_0\) | |||
| \(a_1-a_0\) | |||
| \(a_1\) | \(a_2-2a_1+a_0\) | ||
| \( a_2-a_1\) | \(a_3-3a_2+3a_1-a_0\) | ||
| \(a_2\) | \(a_3-2a_2+a_1\) | ||
| \(a_3-a_2\) | |||
| \(a_3\) |
We can take the difference as many times as we like, but given that a sequence was constructed with only addition, subtraction, multiplication and division i.e. it was a polynomial, there is going to be a point when we can stop taking the difference. The important thing now to realize from this figure is that the difference expression contains the coefficients from the Pascal’s triangle. This is good if we want to take the difference many number of times. The code below utilizes this observation.
/// <summary>
/// Finds the difference between terms in a sequence. By chaging the degree, we can take difference of the differences.
/// </summary>
/// <param name="sequence">The sequence of doubles passed in as a double array.</param>
/// <param name="term">The index of the first term where the diff. should be taken. NB: As the degree increases, the smaller can the term be</param>
/// <param name="degree">The type of difference, i.e. if degree=1, the first difference is taken and if degree=2, the difference of the first difference is taken. </param>
/// <example>If the sequence is {1,2,3,4,...}, term=0, degree=1, we get 1. By changning degree=2, we get 0.</example>
/// <returns>The difference between the terms in the sequence, depending on the degree.</returns>
public static double GetDifference(double[] sequence, int term, int degree)
{
// the pascal's triangle should be optimized. we only need half of the values
double result = 0;
bool evenStart = (term + degree) % 2 == 0 ? true : false;
int j = 0;
for (int i = term + degree; j <= degree; i--)
{
result += Pascal(degree, j) * sequence[i] * (evenStart ? (i % 2 == 0 ? 1 : -1) : (i % 2 == 0 ? -1 : 1));
j++;
}
return result;
}
Before we proceed in finding the next term and ultimately the polynomial describing the nth term, let’s focus our attention on a real world example. Say we have the sequence \(\{n^2\}\) i.e. \(1, 4, 9, 16 \dots\). We assume that we don’t know the nth term, i.e. we only know some values of the sequence. The common procedure in this case is to look at the differences, similar to the previous section. For example,
| \(1\) | |||
| \(3\) | |||
| \(4\) | \(2\) | ||
| \( 5\) | \(0\) | ||
| \(9\) | \(2\) | ||
| \(7\) | |||
| \(16\) |
To be sure that we’ve found a pattern, we should end up at zero (assuming a polynomial generated the sequence). The interesting thing about this figure is that we know that each difference in the table can be expressed in terms of the difference expressions in the previous section. So, \(3=(4)-(1)\) and \(2 = (9)-2\times (4)+(1)\). This idea hints us to a possible way of finding the next term in the sequence. Since we know that the second difference \(2\) is constant, we can find an expression for the next term by some simple arithmetic. That is, \(2=a_n -2\times a_{n-1} + a_{n-2}\). Thus we can find the nth term given the two terms before it. This is done by the following code:
/// <summary>
/// Finds the next term in the sequence, given that a pattern exist.
/// </summary>
/// <param name="sequence">The sequence of doubles passed in as a double array.</param>
/// <param name="term">If term=-1, the next term in the sequence is going to be found. By default, you don't need to change this variable.</param>
/// <returns></returns>
public static double GetNextTerm(double[] sequence, int term = -1)
{
int constantIndex = 0;
if (HasPattern(sequence, out constantIndex))
{
double constant = GetDifference(sequence, 0, constantIndex - 1);
if (term == -1)
{
// have find the term to start with to figure out the n+1 term.
term = sequence.Length - constantIndex;
}
double result = 0;
bool evenStart = (term + constantIndex - 1) % 2 == 0 ? true : false;
int j = 1;
result += constant;
for (int i = term + constantIndex - 1; j <= constantIndex - 1; i--)
{
result += Pascal(constantIndex - 1, j) * sequence[i] * (evenStart ? (i % 2 == 0 ? 1 : -1) : (i % 2 == 0 ? -1 : 1));
j++;
}
return result;
}
throw new Exception("The sequence does not contain a recognized pattern.");
}
This is a bit more tricky to find in contrast to what we’ve done so far. The nth term is very dependent on the number of times the difference operation has to be taken before we end up at zero. In the previous example, we had to take it three times to get to zero. The polynomial we got had the second degree. It turns out that if we had to take the difference \(n\) times to get to zero, the polynomial is of the degree \(n-1\). This is quite useful, because if we know how the polynomial looks like, the only thing we need to find are the coefficients (more in-depth tutorial).
In the sequence \(1,4,9,16\dots\), we had to take the difference three times, so the polynomial has the second degree, i.e. \(ax^2+bx+c\). We have three unknowns, so we need three data points to solve the system of equations. That is,
\(\left[ {\begin{array}{*{20}{c}} 1 & 1 & 1 & 1 \\ 4 & 2 & 1 & 4 \\ 9 & 3 & 1 & 9 \end{array}} \right]\)
When we reduce this matrix to echelon form, we get that the coefficient for \(n^2 \) is \(1\), and zero for the remaining terms. The code below does this task.
/// <summary>
/// Finds the coefficients of the nth term and returns them in a double array. The first item in the array is of the highest power. The last term in the array is the constant term.
/// </summary>
/// <param name="sequence">The sequence of doubles passed in as a double array.</param>
/// <param name="degree">The degree value returned here is the number of times we have to take the differnce of this sequence (using GetDifference) to get the difference to be zero.</param>
/// <returns></returns>
public static double[] GetCoefficientsForNthTerm(double[] sequence, int degree)
{
var mat = new Matrix(degree, degree + 1);
for (int i = 0; i < degree; i++)
{
for (int j = 0; j <= degree; j++)
{
if (j == degree)
{
mat[i, j] = sequence[i];
}
else
{
mat[i, j] = Get.IntPower(i + 1, (short)(degree - j - 1));
}
}
}
mat.RREF();
var output = new double[degree];
for (int i = 0; i < degree ; i++)
{
output[i] = mat[i, degree];
}
return output;
}
The coefficients we get correspond to a term in the polynomial. For example, if we get \(3, 2, 1\), the polynomial is \(3x^2+2x+1\).
When we first think about how we can find the closed form for a sum, we might conclude that it is difficult. In Concrete Mathematics – A Foundation for Computer Science, an entire chapter (chp. 2) and a great part of other chapters is dedicated to sums, and the way we can find the anti-difference. At least, that was my thought when I got this idea. But later, an interesting thought came up to my mind, and that is to treat the sum as a sequence and the sequence as the difference of the sums’ terms. Let’s clarify this. If we have the sequence \( 1,2,3,4,\dots\), we can construct the partial sums, i.e. \(1, 1+2, 1+3+4, 1+2+3+4\), thus \(1, 3, 6, 10\). But the partial sums form a new sequence which we can analyse in a similar way. This means that can we can reuse quite a lot of code. Now, since in the original sequence \( 1,2,3,4,\dots\), we have to take the difference twice to get zero, in the new sequence \(1, 3, 6, 10\), we have to take the difference three times. The code for doing this is shorter, in contrast to the previous ones.
/// <summary>
/// Finds the coefficients of the closed form of the sum and returns them in a double array. The first item in the array is of the highest power. The last term in the array is the constant term.
/// </summary>
/// <param name="sequence">The sequence of doubles passed in as a double array.</param>
/// <param name="degree">The degree value returned here is the number of times we have to take the differnce of this sequence (using GetDifference) to get the difference to be zero.</param>
/// <returns></returns>
public static double[] GetCoefficientsForNthSum(double[] sequence, int degree)
{
double[] partialSums = new double[sequence.Length];
partialSums[0] = sequence[0];
for (int i = 1; i < sequence.Length; i++)
{
partialSums[i] = partialSums[i - 1] + sequence[i];
}
return GetCoefficientsForNthTerm(partialSums, degree + 1);
}
One of the limitations of this code/algorithm is that we can only use sequences that have been generated by a polynomial. Exponents are not allowed, although \(n^2= n\times n\), so that works. The reason is quite simple. Formally, we define difference as an operator on a function (similar to derivatives) as
\(\Delta f(x) = f(x+1) – f(x)\). Let’s say we have \(f(x)=2^x\). If we take \(\Delta(2^x)=2^{x+1}-2^x=2^x(2-1)=2^x\). Not good, no matter how many times we take the difference, we end up with the same thing we had in the beginning. This is why this particular algorithm does not work in this case. It is possible to add an extra step that checks against known sequences each time a difference is taken. This, I will do a bit later! 🙂
You can find all additional methods in the FiniteCalculus class in Mathos.Calculus (Mathos Core Library). Also, you can see this code in action here!
During the 2 hours journey to Stockholm from Bjursås, I found an interesting way of illustrating solutions to problems with a certain pattern. In this case, it was a recursion problem. The problem is as following (From Concrete Mathematics – A Foundation for Computer Science 2nd edition):
Problem
Solve the recurrence:
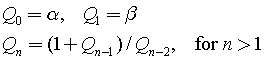
Assume that
![]()
Solution
When we look at several cases a pattern is going to be observed quite quickly.
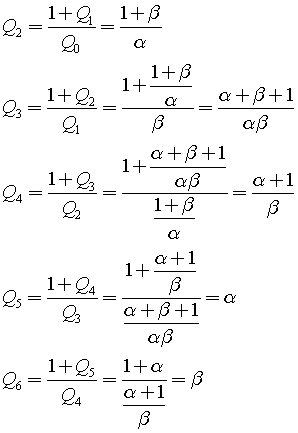
As you might see, the fifth and sixth terms turn out to be the initial conditions that were set in the beginning (see the first and second terms). Therefore, this recurrence will produce a repeating pattern.
The question we face at this stage is how the following can be described as a single expression.
My solution consists of five main steps:
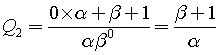
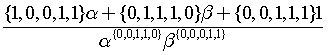 .
.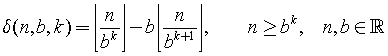
Note, δ(3, 2, 4-i) can be written as δ(3, 2, i) if the loop starts at i=4 and ends at i=0. Therefore,
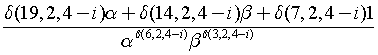
or if we reverse the loop
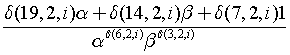
Conclusion
Initially, this problem was all about to find a pattern in a recurrence. However, by trying to generalize the pattern in another way, new perspectives of looking at the pattern were found. Now, instead of stating the pattern with words, we can express it in a very condensed form. Moreover, the solution can be said to have several levels of abstractions. We have, in other words, modularized the problem into 1) a function that finds digit in base 2 – “the delta function” and 2) a common expression that uses the function to express the pattern. The group of 1 and 2 can be another abstraction level, i.e. we can now use this to solve other recurrences without going in to details of each individual part.
I think and hope that this way of looking at the problem will allow us to analyse different patterns more in details and find even more patterns that we have not thought about!
Additional links/resources
Ruby code
#the floor can be removed if n and b # are integers. def f(n,b,k) (n/b**k).floor - b*(n/b**(k+1)).floor end (0..4).each do |i| print f(3,2,4-i) end
The requirement of performing several thousands of calculations (for example, during integration) led to the optimization with pre-scanned expressions. But the aim to make Mathos Parser even faster still remained. Now, I would like to introduce you to a new project of Mathos Project – Mathos Expression Compiler, based on the math tokenizer and parser logic of Mathos Parser.
This API allows you to parse an expression and “store” it as CIL code. Then, using ILAsm, you can generate a new assembly that will contain your expression entirely parsed. The only operation that occurs at runtime is the insertion of values into the variables that you declared and the operation on that variable value. To make it even faster, most of the calculations are already done before the runtime, for example, x+3+5 would be stored as x+8.
In this scenario, the time consideration can be important. Even if it is faster to execute CIL instructions, the compilation process can take some time. This has not been tested yet. The process is illustrated below:
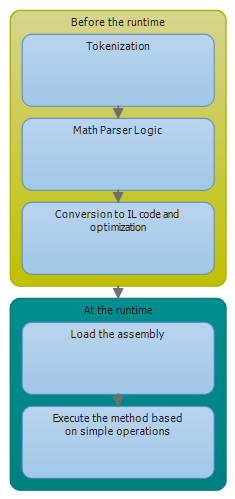
This is a very simplified way of looking at it but the point is to always test Mathos Parser together with Mathos Expression Compiler and make an estimate of how much time would be saved in different scenarios. It all depends on the context. But note, that
A performance hit is incurred only the first time the method is called. All subsequent calls to the method execute at the full speed of the native code because verification and compilation to native code don’t need to be performed again. //p. 12. Jeffrey Richter. CLR via C# 3rd Edition
So, if you plan to execute the function trillion times, it might be a good a idea to keep in mind the Expression Compiler as a better alternative, because at that point, the compilation time will be negligible.
Now, back to the features. It was mentioned in the beginning that it is based on the Mathos Parser. Note, in terms of features, Mathos Expression Compiler has at this point only a subset of those of Mathos Parser. At this point, you cannot have functions as sin, cos, and your own custom functions, but this will be changed in the nearest future.
There are also some changes to the way operators work. To declare an operator properly, you should use the variables OperatorList, OperatorAction, and OperatorActionIL. Below, a simple example of addition operator:
OperatorList.Add("+"); // addition
OperatorActionIL.Add("+", "call valuetype [mscorlib]System.Decimal [mscorlib]System.Decimal::op_Addition(valuetype [mscorlib]System.Decimal,valuetype [mscorlib]System.Decimal)");
OperatorAction.Add("+", (x, y) => x + y);
Comparison operators are a bit more tricky. An example of greater than operator is shown below:
OperatorList.Add(">"); // greater than
OperatorActionIL.Add(">", "call bool [mscorlib]System.Decimal::op_GreaterThan(valuetype [mscorlib]System.Decimal,valuetype [mscorlib]System.Decimal)\r\n" +
"brtrue.s q@\r\n" +
"ldc.i4.0 \r\n" +
"br.s p@\r\n"
+ "q@: ldc.i4.1\r\n"
+ "p@: nop\r\n"
+ "call valuetype [mscorlib]System.Decimal [mscorlib]System.Decimal::op_Implicit(int32)");
OperatorAction.Add(">", (x, y) => x > y ? 1 : 0);
For those who understand IL, the @ sign might seem a bit strange. It is simply a way to tell the stack count to the if statement (in the compilation process).
When you actually generate an expression, this is how your IL code for that expression might look:
var mp = new Mathos.ILParser.ILMathParser();
mp.LocalVariables.Add("x");
mp.LocalVariables.Add("y");
string a = mp.Parse("(x(3x))");
Will return (only IL for the expression):
.maxstack 5 .locals init(valuetype [mscorlib]System.Decimal, valuetype [mscorlib]System.Decimal) ldc.i4 3 ldc.i4 0 ldc.i4 0 ldc.i4 0 ldc.i4 0 newobj instance void [mscorlib]System.Decimal::.ctor(int32,int32,int32,bool,uint8) stloc.0 ldloc.0 ldarg.0 call valuetype [mscorlib]System.Decimal [mscorlib]System.Decimal::op_Multiply(valuetype [mscorlib]System.Decimal,valuetype [mscorlib]System.Decimal) stloc.1 ldloc.1
When you have the IL code, you should name the output executable(or dll) as MathosILParser, otherwise, you might get an error. In future, an option will be added to customize the name of the output file, but at this point, please use RegEx (or replace option) to change the MathosILParser.exe to something else (in the IL code).
Your function can later by called as shown below. Note, I am not using reflection at all.
decimal result = Mathos.ILFunction.Parse(3, 2);
I hope this short guide was helpful, even if it might be a bit messy. If you have performed any testing related to speed or if you want to show some examples, please feel free to comment or contact me.
The article, Introduction to IL Assembly Language, is a great resource for those of you who would like to understand IL code (kind of like asm but in .net). IL really gives you a different perspective on computer programming, and you must consider more things in comparison to high level languages like C#.
Currently, I am studying conditional statements. Below, an example of a statement that checks whether the two values in the evaluation stack are equal to each other.
//An example of an if statement.
.assembly extern mscorlib {}
.assembly Test
{
.ver 1:0:1:0
}
.module test.exe
.method static void main() cil managed
{
.maxstack 2
.entrypoint
ldc.i4 30
ldc.i4 40
beq Equal
ldstr "No, they are not equal"
call void [mscorlib]System.Console::WriteLine (string)
br Exit
Equal:
ldstr "Yes, they are equal"
call void [mscorlib]System.Console::WriteLine (string)
Exit:
ret
}
By executing this, the result below would be shown:
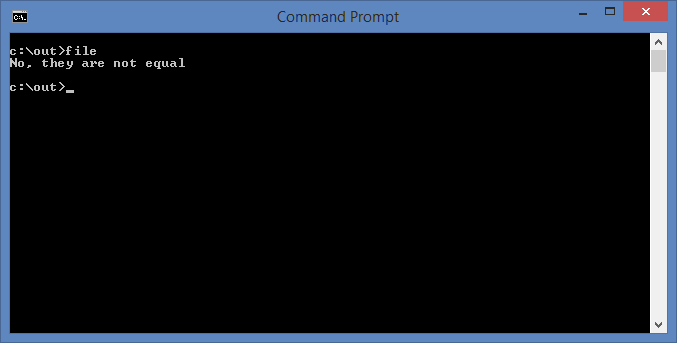
RubyInt project, or Iron Ruby Based Mathos Core Library Interpreter was one of the projects to be tested with the new parser feature, that is, pre-scanned expressions.
In the Integral approximation module, it is quite good to use pre-scanned expressions, since the expression stays the same through the entire process. The execution time improved in this case.
The integral approximation website in Mathos Laboratory (see it here) has also shown good results thanks to this optimization. In Mathos Laboratory in particular, it is important that methods are quick and use as small amount of resources as possible, because it is hosted in the Cloud.
I have performed some quick tests using an i3 processor (the methods are in changeset 37964), although I would not recommend them to draw specific conclusions (there is a random error involved so more repetitions of each test are needed). Also, the difficulty level of an expression can affect the tokenization time. The graphs are located below:
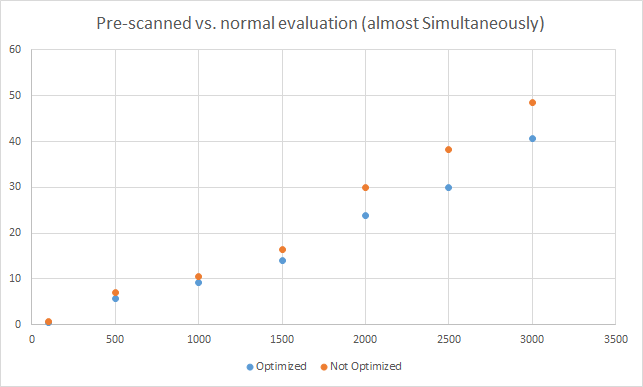
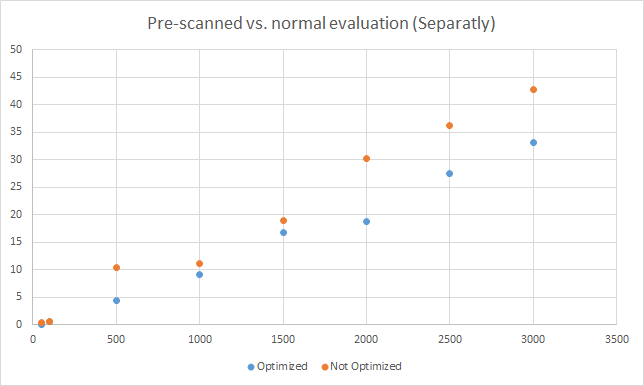
One conclusion that can be drawn from this is that the optimization only gets useful when the same expression is evaluated more than 100-500 times.
[This article was updated to included changes in v. 1.0.7.2. Originally written for v. 1.0.7.1]
Today, I published a newer version of Mathos Parser on both CodePlex and NuGet. The release notes:
from v.1.0.7.2:
- Force user to use ReadOnlyCollection when using a token list as a parameter.
from v. 1.0.7.1
- Added method GetTokens
- Changed the structure a bit. Now, the Scanner returns tokens instead of continuing with MathParserLogic. This is good if the same kind of expression is to be used many times.
But what does this really mean? Well, previous versions of the parser worked more locally, that is, once one function was executed, it triggered another function, and so on. Now, however, the Scanner (private method) returns a list of tokens instead of launching MathParserLogic directly. If you simply want to get tokens, you would have to execute the GetTokens function, as shown below:
var parser = new MathParser();
parser.LocalVariables.Add("x",10);
var list = parser.GetTokens("(3x+2)");
You can then send the tokens list into either Parse or ProgrammaticallyParse and it will parse it in the same way as if you would enter a string expression, that is:
decimal resultA = parser.Parse("(3x+2)");
decimal resultB = parser.Parse(list);
Both statements above will return 32, but there is one main difference; the execution time will be so much smaller for the second statement, where a “pre-compiled” list is being used. If it would take 100 milliseconds (ms) to find the value of the first statement, it would take approximately 9-10 ms for the second one. The ratio is 10:1.
This is great if you want to perform an operation where the same function is involved several thousands times, for example when approximating an integral.
I am currently thinking about converting math expressions into IL code, but this will happen sometime in future!
In order to emphasize the ability to control an application when online key validation is being used, I have created a poster. Serial Key Manager be found here.
It is important to have a logo to connect different things together (websites, blogs, programs). After some hours of work I managed to create one:
Although I had some other drafts, I think this is the one I am going to use!
In this article, I would like to find out whether it is possible to construct a programming language with Mathos Parser. In general, the question is if a simple expression parser has the necessary things to easily convert it into a language.
The answer is yes, but the language will be very limited if additional features are not added. The reason for this is because what most languages have in common is some sort of user/machine interaction, while an expression parser only allows you to parse mathematical things and is not really designed to interpret how to write to a file or allocate memory.
For example, imagine you want to create something similar to if statements and you decide to treat an if as a function. You would use following code:
parser.LocalFunctions.Add("if", x =>
{
if (x[0] == 1)
{
return x[1];
}
else
{
if (x.Length == 3)
{
return x[2];
}
else
{
return 0;
}
}
});
So, if whatever we pass into the first parameter is true, the value in the second parameter will be returned. This is quite cool, but it does not allow us to return a series of statements. Instead, we could design a new kind of if statement that would, depending on the result from this if function, execute the right method. Here is how I solved it:
let a = get() # ask for user input if(a>3,1, 0) # it only returns a number 1-> write It is true # these execute something depending on result 0-> write It is false
As you can see, the if statement is still there, but there is now a feature that will interpret the result and make something happen. You can also use \n to separate between different statements and also name a collection of statements, as shown below:
# Using statements as small methods # The first result will not use statement, # the second one will. notTrue : title Not true \n write Your number is smaller than five (or equal to) \n pause write Type a number between 1-10 let b be get() if(b>5, 1, 0) 1-> title A New title! \n write Your number is greater than five! \n pause 0-> notTrue
Note that both examples use a function get(). It can also be implemented as a function:
parser.LocalFunctions.Add("get", x =>
{
return System.Convert.ToDecimal(Console.ReadLine());
}
);
You might have noticed the use of statements (see notTrue statement). Their role is to simulate a method. Everything you enter into a statement will not be executed until you call it, so you can insert undefined variables into a statement when you define it and later assign them with a value. I have also added commands like write, title, pause, clear and end. These are extensions to the language and are interpreted in the method below:
static void command(Mathos.Parser.MathParser parser, string input, Dictionary<string, string> statement, ref decimal lastResult)
{
try
{
input = Regex.Replace(input, "#\\{.*?\\}#", ""); // Delete Comments #{Comment}#
input = Regex.Replace(input, "#.*$", ""); // Delete Comments #Comment
input = Regex.Replace(input, @"[0-9]+\!", new MatchEvaluator(FactorialString));
input = Regex.Replace(input, @"^\s+", "");
if (input != "")
{
if (input.StartsWith("write"))
{
Console.WriteLine(input.Substring(6));
}
else if (input.StartsWith("title"))
{
Console.Title = input.Substring(6);
}
else if (input.StartsWith ("clear"))
{
Console.Clear();
}
else
{
if (input.Contains("->"))
{
int index = input.IndexOf("->");
if (lastResult == System.Convert.ToDecimal(input.Substring(0, index)))
{
mCommand(parser, input.Substring(index + 2), statement, ref lastResult);
}
}
else
{
if (input.Contains(":") && input.Contains(":=") == false)
{
int index = input.IndexOf(":");
statement.Add(input.Substring(0, index).Replace(" ", ""), input.Substring(index + 1, input.Length - index - 1));
}
else if (input.StartsWith("pause"))
{
Console.ReadKey();
}
else if (input.StartsWith("end"))
{
Environment.Exit(0);
}
else
{
foreach (var item in statement)
{
if (input.Contains(item.Key))
{
input = "";
mCommand(parser, item.Value, statement, ref lastResult);
}
}
lastResult = parser.ProgrammaticallyParse(input, identifyComments: false);
Console.WriteLine(lastResult);
}
}
}
}
}
catch (Exception e)
{
Console.WriteLine("An error occured. Message: " + e.Message);
}
}
static void mCommand(Mathos.Parser.MathParser parser, string input, Dictionary<string, string> statement, ref decimal lastResult)
{
input = input.Replace(@"\n", System.Environment.NewLine);
System.IO.StringReader sr = new System.IO.StringReader(input);
string _input = sr.ReadLine();
while (_input != null)
{
command(parser, _input, statement, ref lastResult);
_input = sr.ReadLine();
}
sr.Close();
}
Some programmers will certainly argue that the code above is not that optimized and is quite primitive. Well, it serves its purpose and makes Mathos Parser look more like a language.
In the next article I want to implement a while feature into this awesome programming language.
Conclusion: Just because something can parse expressions does not mean it can parse a series of statement. In order to fix this we can either choose to add some features externally, or, go into the parser itself and make it more adjusted to this particular task. This language does not alter Mathos Parser in any way.
Downloads:
